Python 实现作业排程问题

1. 问题描述

• Automobile factory with two assembly lines
  • Each line has n stations: $S_{1, 1},...,S_{1, n}$ and $S_{2, 1},...,S_{2, n}$
  • Corresponding stations $S_{1, j}$ and $S_{2, j}$ perform the same function but can take different amounts of time $a_{1, j}$ and $a_{2, j}$
  • Entry times $e_1$ and $e_2$ and exit times $x_1$ and $x_2$

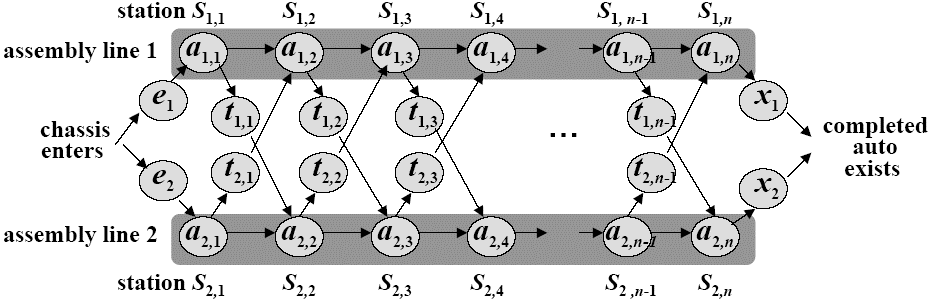
给出一个示例的装配线，要求输出最优的排程方案

2. 思路分析

首先, 利用动态规划思想找出递归关系, 这个是最重要的一步

这里的 $f_1[j]$ 表示在第一条装配线的第 j 个站台处理完之后所花费的最少的时间. $f_2[j]$ 也是同理.

然后, 根据这个关系, 我们就可以自底向上构建 $f_1$ 和 $f_2$ 这两个数组了.

伪码描述如下

3. 代码实现

# 最优排程问题
def fastest_way(a:list, t:list, e:list, x:list, n:int) -> list:
    '''
    解决最优排程问题
    :param a: 两条线上各自的每个站点的各自处理时间
    :param t: 两条线上各自的每个前 n - 1 个站点的切换时间
    :param e: 两条线的各自的 entry 时间
    :param x: 两条线的各自的 exit 时间
    :param n: 每条线的工作站的数目
    :return: 最优时间, 路径和最后一个走过的工作站点
    '''
    # 两条线上每个站的处理时间
    a1, a2 = a # 自动解包
    # 两条线在第 i 个站换线需要的时间
    t1, t2 = t
    # 两条线上 e 和 x 的数值
    e1, e2 = e
    x1, x2 = x
    # 两条线在每个装配点所花费的最小时间表（动态规划）
    f1 = [0 for i in range(n)]
    f2 = [0 for i in range(n)]
    route = [[0 for i in range(n)], [0 for i in range(n)]]  # 存储路径
    time = float('inf') # 最优时间
    final_line = 0 # 最后一个节点所在的线路
    # 初始化
    f1[0] = e1 + a1[0]
    route[0][0] = 1 # 1 表示走第一条线路
    f2[0] = e2 + a2[0]
    route[1][0] = 2 # 2 表示走第二条线路
    for i in range(1, n):
        if f1[i - 1] + a1[i] < f2[i - 1] + t2[i - 1] + a1[i]:
            f1[i] = f1[i - 1] + a1[i]
            route[0][i] = 1
        else:
            f1[i] = f2[i - 1] + t2[i - 1] + a1[i]
            route[0][i] = 2
        if f2[i - 1] + a2[i] < f1[i - 1] + t1[i - 1] + a2[i]:
            f2[i] = f2[i - 1] + a2[i]
            route[1][i] = 2
        else:
            f2[i] = f1[i - 1] + t1[i - 1] + a2[i]
            route[1][i] = 1
    if (f1[n - 1] + x1 < f2[n - 1] + x2):
        time = f1[n - 1] + x1
        final_line = 1
    else:
        time = f2[n - 1] + x2
        final_line = 2
    return [time, route, final_line]

def print_route(i:int, j:int, route:list, n:int):
    '''
    递归打印装配的线路图
    :param i: 装配线, 0 represents the first assembly line, 1 represents the second line
    :param j: 当前节点
    :param route: 存储两条线路的节点的父节点的 list
    :param n: 装配线的节点数
    :return: None
    '''
    if j == 1:
        print('[Line: ' + str(i) + ' Station: ' + str(j) + ']', end=' ')
    else:
        print_route(route[i - 1][j - 1], j - 1, route, n)
        print('[Line: ' + str(i) + ' Station: ' + str(j) + ']', end=' ')
    if j != n:
        print('=>', end=' ')
    else:
        print()

if __name__ == '__main__':
    n = 5  # 每条线工作站的数目
    # 两条线上每个站的处理时间
    a1 = [7, 9, 3, 4, 8]
    a2 = [8, 5, 6, 4, 5]
    # 两条线在第 i 个站换线需要的时间
    t1 = [2, 3, 1, 3]
    t2 = [2, 1, 2, 2]
    # 两条线上 e 和 x 的数值
    e1 = 2
    e2 = 4
    x1 = 3
    x2 = 6
    a = [a1, a2]
    t = [t1, t2]
    e = [e1, e2]
    x = [x1, x2]
    res = fastest_way(a, t, e, x, n)
    time, route, final_line = res
    print('The shortest time:', time)
    print('The best assembly line is: ', end='')
    print_route(final_line, 5, route, n)

输出

The shortest time: 35
The best assembly line is: [Line: 1 Station: 1] => [Line: 2 Station: 2] => [Line: 1 Station: 3] => [Line: 1 Station: 4] => [Line: 1 Station: 5]