单源最短路径之 Bellman-Ford 算法详解及其 Python 实现
前言
本博客的内容基本来自《算法导论》。
算法描述
Bellman-Ford
算法解决的是一般情况下的单源最短路径问题,在这里,边的权重可以为负值。给定带权重的有向图
$G = (V, E)$ 和权重函数
$\omega : E \rightarrow \mathbf{R}$,Bellman-Ford
算法返回一个布尔值,以表明是否存在一个从源结点可以到达的权重为负值的环路。如果存在这样一个环路,算法将告诉我们不存在解决方案。如果没有这种环路存在,算法将给出最短路径和它们的权重。
Bellman-Ford 算法通过对边进行松弛操作来渐近地降低从源结点
$s$ 到每个结点 $v$ 的最短路径的估计值
$v.d$,直到该估计值与实际的最短路径权重
$\delta(s, v)$ (注二)相同时为止。该算法返回 TRUE
值当且仅当输入图中不包含可以从源结点到达的权重为负值的环路。
伪码描述如下

算法运行的一个示例图
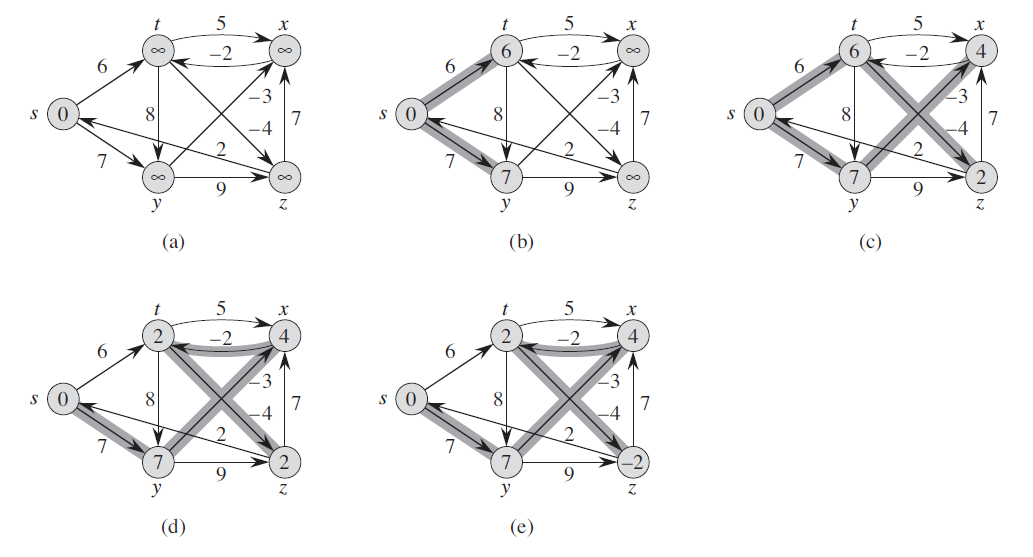
对上图的说明:源结点为 $s$,结点中的数值为该结点的
$d$(注一)值,加了阴影的边比奥氏前驱值:如果
$(u, v)$ 加了阴影,则
$v.\pi = u$。在本图的例子中,每一次的松弛操作对边的处理次序都是:$(t, x)$,$(t, y)$,$(t, z)$,$(x, t)$,$(y, x)$,$(y, z)$,$(z, x)$,$(z, s)$,$(s, t)$,$(x, y)$,(a)
在第 1 次松弛操作前的场景。(b) ~ (e) 在对边进行每次松弛操作后的场景。图
(e) 中的 $d$ 值和 $\pi$
值为最终取值。在本例中,Bellman-Ford 算法返回的值为 TRUE。
补充
对边的松弛操作(Relax)
注一:$d$ 是结点的一个属性,比如,$v.d$
记录的是从源结点 $s$ 到结点 $v$
之间的距离。同理, $\pi$
也是结点的一个属性,比如,$v.\pi$ 记录的是 $v$
的前驱结点。(见《算法导论》中文版 p344)
注二:定义从结点 $u$ 到结点 $v$
的最短路径权重 $\delta(u, v)$ 如下
$$
$$