最小生成树的 Prim 算法(未竟)

算法思路

以图1来说明

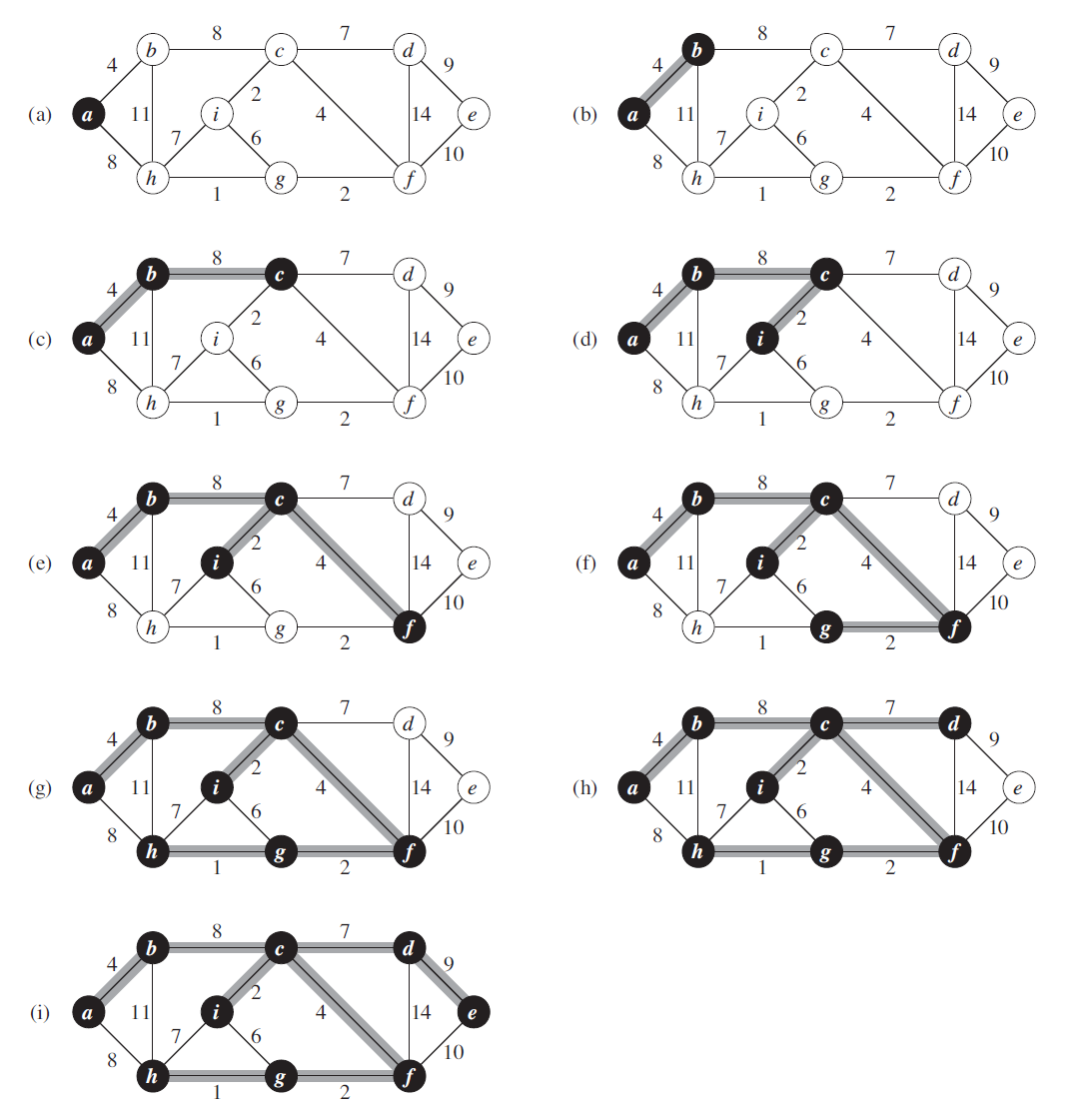
上图演示了执行 Prim 算法的过程。初始的根结点为 a。加阴影的边和黑色的结点都属于树 A。在算法每一步，树中的结点就决定了图的一个切割，横跨该切割的一条轻量级边被加入到树中。例如，在图中的第 2 步，该算法可以选择将边(b, c)加入到树中，也可以选择将边(a, h)加入到树中，因为这两条比那都是横跨该切割的轻量级边。

伪码

补充

这里对一些定义作补充。

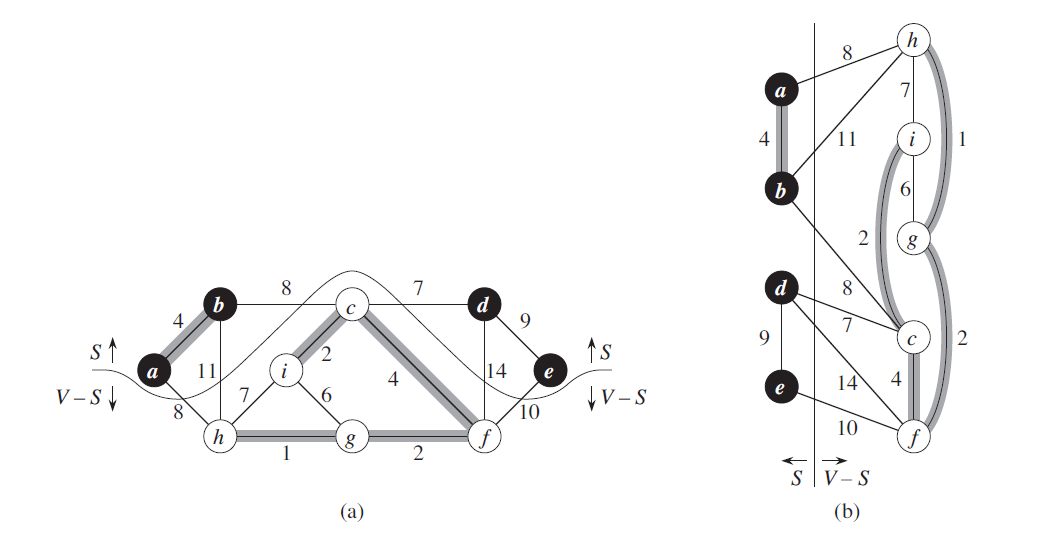
无向图 $G = (V, E)$ 的一个切割 $(S, V - S)$ 是集合 $V$ 的一个划分，如图3所示。如果一条边 $(u, v) \in E$ 的一个端点位于集合 $S$，另一个端点位于集合 $V - S$，则称该条边横跨切割 $(S, V - S)$。如果集合 $A$ 中不存在横跨该切割的边，则称该切割尊重集合 $A$。在横跨一个切割的所有边中，权重最小的边称为轻量级边。注意，轻量级边可能不是唯一的。一般，如果一条边是满足某个性质的所有边中权重最小的，则称该条边是满足给定性质的一条轻量级边。