《编译原理第三版》（张素琴）学习札记

记载本书所有章节的阅读札记。

第二章

何为符号 $\Rightarrow$？

符号 $\Rightarrow$ 的含义是，使用一条规则，代替左端的某个符号，产生其右端的符号串。

何为规则？

规则，也称重写规则、产生式或生成式，是形如 $\alpha \rightarrow \beta$ 或 $\alpha ::= \beta$ 的有序对，其中 $\alpha$ 称为规则的左部，$\beta$ 称作规则的右部。

设某一文法 $G$，何为文法 $G$ 的字母表？

\[V_N \cup V_T = \varnothing\]

通常用 $V$ 表示 $V_N \cup V_T$，$V$ 称为文法 $G$ 的字母表或词汇表。

关于符号 $\rightarrow$ 或 $::=$？

符号 $\rightarrow$ 或 $::=$ 读作“定义为”。

例如，$A \rightarrow a$ 读作“$A$ 定义为 $a$”。也把它说成是一条关于 $A$ 的规则（产生式）。

何为四元组？

文法 $G$ 定义为四元组 $\displaystyle{(V_N, V_T, P, S)}$。

$V_N$：非终结符（或语法实体，或变量）集；
$V_T$：终结符集；
$P$：规则 $(\alpha \rightarrow \beta)$ 的集合
- $\alpha \in (V_N \cup V_T)^{*}$ 且至少包含一个非终止符
- $\beta \in (V_N \cup V_T)^{*}$；
$V_N, V_T, P$ 是非空有穷集；
$S$ 称作识别符或者开始符，它是一个非终结符，至少要在一条规则中作为左部出现。

关于文法 $G$ 的一些规定？

一般约定，第一条产生式的左部是识别符；
用尖括号括起来的是非终结符，不用尖括号括起来的是终结符；
或者用大写字母表示非终结符，小写字母表示终结符；
另外，还有一种习惯写法，将 $G$ 写成 $G[S]$，其中 $S$ 是识别符。

何为 0 型文法？

设 $G = (V_N, V_T, P, S)$，如果它的每一个产生式 $\alpha \rightarrow \beta$ 是这样一种结构：$\alpha \in (V_N \cup V_T)^*$ 且至少含有一个非终结符，而 $\beta \in (V_N \cup V_T)^*$，则 $G$ 是一个 0 型语法文法。

0 型文法也称短语语法。

何为 1 型文法？

设 $G = (V_N, V_T, P, S)$ 为一个文法，若 $P$ 中的每一个产生式 $\alpha \rightarrow \beta$ 均满足 $|\beta| \geqslant |\alpha|$，仅仅 $S \rightarrow \varepsilon$ 除外，则文法 $G$ 是 1 型 或 上下文有关的（context-sensitive）。

何为 2 型文法？

设 $G = (V_N, V_T, P, S)$。若 $P$ 中的每一个产生式 $\alpha \rightarrow \beta$ 满足：$\alpha$ 是一个非终结符，$\beta \in (V_N \cup V_T)^*$，则此文法称为 2 型的 或 上下文无关的（context-free）

何为 3 型文法？

设 $G = (V_N, V_T, P, S)$，若 $P$ 中的每一个产生式的形式都是 $A \rightarrow aB$ 或 $A \rightarrow a$，其中 $A$ 和 $B$ 都是非终结符，$a \in V_T^*$，则 $G$ 是 3 型文法 或 正规文法。

问题：P25，上下文有关法的等价定义的理解？

似乎 $A$ 在 $V_N$ 中，是单个字符。

何为符号 $\mathop{\Rightarrow}\limits^{+}$？

如果存在直接推导的序列：\[v = w_0 \Rightarrow w_1 \Rightarrow w_2 \Rightarrow \cdots \Rightarrow w_n = w \; (n > 0)\] 则称 $v$ 推导出（产生）$w$（推导长度为 $n$），或称 $w$ 归约到 $v$，记作 $v \mathop{\Rightarrow}\limits^{+} w$。

若有 $v \mathop{\Rightarrow}\limits^{+} w$，或 $v = w$，则记作 $v \mathop{\Rightarrow}\limits^{*} w$。

何为句型，何为句子？

设 $G[S]$ 是一个文法，如果符号串 $x$ 是从识别符推导出来的，即有 $S \mathop{\Rightarrow}\limits^{*} x$，则称 $x$ 是文法 $G[S]$ 的句型。

按：注意上面的 $S \mathop{\Rightarrow}\limits^{*} x$ 是 $*$ 闭包，所以 $S$ 本身也是句型。

若 $x$ 仅由终结符号组成，即 $S \mathop{\Rightarrow}\limits^{*} x, \; x \in V_T^*$，则称 $x$ 为 $G[S]$ 的句子。

何为 $L(G)$？

文法 $G$ 所产生的语言定义为集合

\[ \{ x| S \mathop{\Rightarrow}\limits^* x, 其中 S 为文法识别符号，且 x \in V^*_T\} \]

可用 $L(G)$ 表示该集合。

何为文法的二义性？

如果一个文法存在某个句子对应两棵不同的语法树，则说这个语法是二义的。或者说，若一个文法中存在某个句子，它有两个不同的最左（最右）推导，则这个语法是二义的。

举例：文法 $G = (\{ E \}, \{ +, *, i, (, ) \}, P, E)$，其中 $P$ 为：

\[ \begin{align} &E \rightarrow i \\ &E \rightarrow E + E \\ &E \rightarrow E * E \\ &E \rightarrow (E) \end{align} \]

对于这个文法 $G$，句型 $i * i + i$ 有两个不同的最左推导 1 和 2，它们的语法树如下：

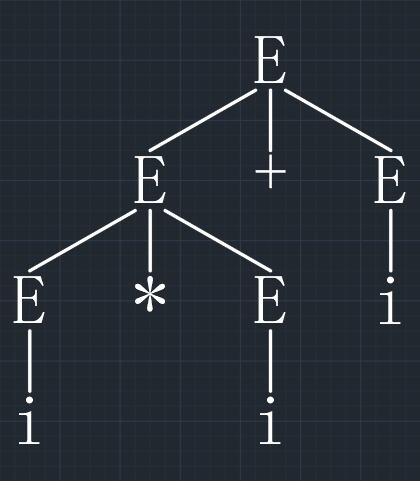
推导 1 的语法树

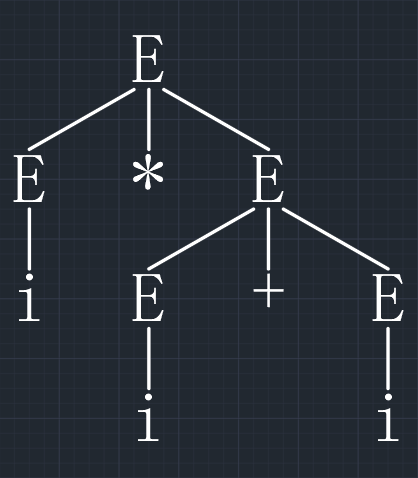
推导 2 的语法树

\[ \begin{align} &推导 1：E \Rightarrow E + E \Rightarrow E * E + E \Rightarrow i * E + E \Rightarrow i * i + E \Rightarrow i * i + i \\ &推导 2：E \Rightarrow E * E \Rightarrow i * E \Rightarrow i * E + E \Rightarrow i * i + E \Rightarrow i * i + i \end{align} \]

何为最左推导、最右推导、规范推导、右句型、规范句型？

如果在推导的任何一步 $\alpha \Rightarrow \beta$，其中，$\alpha$、$\beta$ 是句型，都是对 $\alpha$ 中的最左非终结符进行替换，则称这种推导为最左推导。

如果在推导的任何一步 $\alpha \Rightarrow \beta$，其中，$\alpha$、$\beta$ 是句型，都是对 $\alpha$ 中的最右非终结符进行替换，则称这种推导为最右推导。

在形式语言中，最右推导常被称为规范推导。

由规范推导所得的句型称为右句型或规范句型。

何为短语、直接短语、和句柄？

令 $G$ 是一个文法，$S$ 是文法的开始符号，$\alpha \beta \delta$ 是文法 $G$ 的一个句型。如果有 $S \mathop{\Rightarrow}\limits^* \alpha A \delta$ 且 $A \mathop{\Rightarrow}\limits^+ \beta$，则称 $\beta$ 是句型 $\alpha \beta \delta$ 相对于非终结符 $A$ 的短语。

特别地，如果有 $A \Rightarrow \beta$，则称 $\beta$ 是句型 $\alpha \beta \delta$ 相对于规则 $A \rightarrow \beta$ 的直接短语（也称简单短语）。

一个右句型的直接短语称为该句型的句柄。句柄的概念只适用于右句型。

最后两个定理要再看看。

第三章

何为正规文法？

这个概念在第二章有讲过，这里再次摘录一下。

正规文法也称为 3 型文法 $G = (V_N, V_T, S, P)$，其 $P$ 中的每一条规则都有下述形式：$A \rightarrow aB$ 或 $A \rightarrow a$，其中 $A, B \in V_N, \; a \in V_T^*$。

正规文法所描述的是 $V_T$ 上的正规集。

何为正规集？

按：本书中似乎没有正规集的概念。遂从《编译原理第二版》黑书摘录其定义如下

可以用一个正则表达式定义的语言叫做正则集合（regular set）。

黑书中的翻译是“正则集合”，其实和“正规集”是一个意思。

结合老师所讲，所谓正规集，可以和前面第二章的语言（$L(G)$）这一概念结合来看，它们表达的东西其实是很类似的，因此，正规集所表达的意思就是正规式（正则表达式）所产生的所有字串的集合。

何为正规式？

正规式也称正则表达式，是表示正规集的工具。

(1). $\varepsilon$ 和 $\varnothing$ 都是 $\Sigma$ 上的正规式，它们所表示的正规集分别为 $\{ \varepsilon \}$ 和 $\varnothing$。
(2). 任何 $a \in \Sigma$，$a$ 是 $\Sigma$ 上的一个正规式，它所表示的正规集为 $\{ a \}$。
(3). 假定 $e_1$ 和 $e_2$ 都是 $\Sigma$ 上的正规式，它们所表示的正规集分别为 $L(e_1)$ 和 $L(e_2)$，那么，$(e_1)$、$e_1|e_2$、$e_1 \cdot e_2$ 和 $e_1^*$ 也都是正规式，它们所表示的正规集分别为 $L(e_1)$、$L(e_1) \cup L(e_2)$、$L(e_1)L(e_2)$ 和 $(L(e_1))^*$。
(4). 仅由有限次使用上述 3 个步骤而定义的表达式才是 $\Sigma$ 上的正规式，仅由这些正规式所表示的符号串的集合才是 $\Sigma$ 上的正规集。

其中的 $|$ 读为“或”；$\cdot$ 读为“连接”；$*$ 读为“闭包”。在不致混淆时，括号可省去，但规定算符的优先顺序为先 $*$，再 $\cdot$，最后 $|$。连接符 $\cdot$ 一般可省略不写。$*$、$\cdot$、和 $|$ 都是左结合的。

正规文法转正规式的 3 条规则？

正规式：$A \rightarrow xy$

正规文法：

\[ \begin{split} A &\rightarrow xB \\ B &\rightarrow y \end{split} \]
正规式：$A \rightarrow x^*y$

正规文法：

\[ \begin{split} A &\rightarrow xB \\ A &\rightarrow y \\ B &\rightarrow xB \\ B &\rightarrow y \end{split} \]
正规式：$A \rightarrow x|y$

正规文法：

\[ \begin{split} A &\rightarrow x \\ A &\rightarrow y \end{split} \]

课堂小问：

\[ A \rightarrow xA \\ A \rightarrow y \]

$x$ 可能是多个 $*$ 闭包的组合。

疑问 P45？

(1). 例 3.3，表示无符号数的正规式似乎有点问题。

可以利用 $\varepsilon A = A$ 来理解。那么，这个式子就是对的。

P45 $(a|b)^* = (a^* b^*)^*$ 如何理解？

可以将 $(a|b)^*$ 展开成类似 $(a|b)(a|b) \cdots (a|b)$ 的形式，然后每一个括号内可以随便是 $a$ 或 $b$。

正规式的代数规律？

\[ \begin{split} &(1) \; r|s = s|r \\ &(2) \; r|(s|t) = (r|s)|t \\ &(3) \; (rs)t = r(st) \\ &(4) \; r(s|t) = rs|rt, \; (s|t)r = sr|tr \\ &(5) \; \varepsilon r = r, \; r\varepsilon = r \\ &(6) \; r|r = r \end{split} \]

将正规文法转换成正规式的 3 条规则？

规则一：

\[ \begin{split} 文法产生式：&A \rightarrow xB \quad B \rightarrow y \\ 正规式：&A = xy \end{split} \]
规则二：

\[ \begin{split} 文法产生式：&A \rightarrow xA|y \\ 正规式：&A = x^*y \end{split} \]
文法产生式：

\[ \begin{split} 文法产生式：&A \rightarrow x \quad A \rightarrow y \\ 正规式：&A = x|y \end{split} \]

何为确定的有穷自动机（$\textrm{DFA}$）？

一个确定的有穷自动机 $M$ 是一个五元组：

\[ M = (K, \Sigma, f, S, Z) \]

其中：

(1) $K$ 是一个有穷集，它的每一个元素称为一个状态。
(2) $\Sigma$ 是一个有穷字母表，它的每一个元素称为一个输入符号，所以也称 $\Sigma$ 为输入符号表。
(3) $f$ 是转换函数，是 $K \times \Sigma \rightarrow K$ 上的映像。例如，$f(k_i, a) = k_j$ $(k_i \in K, k_j \in K, a \in \Sigma)$ 就意味着，当前状态为 $k$、输入字符为 $a$ 时，将转换到下一状态 $k_j$，把 $k_j$ 称作 $k_i$ 的一个后继状态。
(4) $S \in K$，是唯一的一个初态。
(5) $Z \subseteq K$，是一个终态集，终态也称可接受或结束状态。

一个 $DFA$ 可以表示成一个状态图（或称状态转换图）。假定 $DFA \; M$ 含有 $m$ 个状态，$n$ 个输入符号，那么这个状态图含有 $m$ 个节点，每个节点最多有 $n$ 个弧射出，整个图含有唯一一个初态节点和若干个终态节点，初态节点冠以“$\Rightarrow$”或标以“$-$”，终态节点终态节点用双圈表示或标以“$+$”，若 $f(k_i, a) = k_j$，则从状态节点 $k_i$ 到状态节点 $k_j$ 画标记为 $a$ 的弧。

对于 $\Sigma^*$ 中的任何符号串，若存在一条从初态节点到某一终态节点的道路，且这条路上所有弧的标记连接成的符号串等于 $t$，则称 $t$ 可为 $DFA \; M$ 所接受，若 $M$ 的初态节点同时又是终态节点，则空字可为 $M$ 所识别（接受）。
可换一种方式叙述如下：
若 $t ^*, $ $f(S, t) = P$，其中 $S$ 为 $\textrm{DFA M}$ 的开始状态， $P \in Z$，$Z$ 为终态集。则称 $t$ 可为 $\textrm{DFA M}$ 所接受（识别）。

何为不确定的有穷自动机（$\textrm{NFA}$）？

一个不确定的有穷自动机 $M$ 是一个五元组：

\[ M = (K, \Sigma, f, S, Z) \]

其中：

(1) $K$ 是一个有穷集，它的每个元素称为一个状态。
(2) $\Sigma$ 是一个有穷字母表，它的每个元素称为一个输入符号。
(3) $f$ 是一个从 $K \times \Sigma^*$ 到 $K$ 的全体子集的映像，即 $K \times \Sigma^* \rightarrow 2^K$，其中 $2^K$ 表示 $K$ 的幂集。
(4) $S \subseteq K$，是一个非空初态集。
(5) $Z \subseteq K$，是一个终态集。

一个含有 $m$ 个状态和 $n$ 个输入符号的 $\textrm{NFA}$ 可表示成一张状态转换图，这张图含有 $m$ 个状态结点，每个结点可射出若干条箭弧与别的节点相连接，每条弧用 $\Sigma^*$ 中的一个串作标记，整个图至少含有一个初态结点以及若干个终态结点。

何为状态集合 $I$ 的 $\varepsilon\text{-闭包}$？

状态集合 $I$ 的 $\varepsilon\text{-闭包}$，表示为 $\varepsilon \text{-closure(I)}$，定义为一个状态集，是状态集 $I$ 中任何状态 $S$ 经任意条 $\varepsilon$ 弧能到达的状态的集合。

何为状态集合 $I$ 的 $a$ 弧转换？

状态集合 $I$ 的 $a$ 弧转换，表示为 $move(I, a)$，定义为状态集合 $J$，其中 $J$ 是所有哪些可从 $I$ 中的某一状态经过一条 $a$ 弧而到达的状态的全体。

如何将一个 $\textrm{NFA}$ 转换为等价的 $\textrm{DFA}$？

这里介绍的方法就是子集法。

假设 $\textrm{NFA N} =$ $\{K, \Sigma, f, K_0, K_t\}$ 按照如下方法构造一个 $\textrm{DFA M} =$ $(S, \Sigma, D, S_0, S_t)$ 使得 $L(M) = L(N)$：

(1) $M$ 的状态集 $S$ 由 $K$ 的一些子集（构造 $K$ 的子集见下图）组成。用 $[S_1, S_2, ..., S_j]$ 表示 $S$ 的元素，其中 $S_1, S_2, ..., S_j$ 是 $K$ 的状态。并且约定，状态 $S_1, S_2, ..., S_j$ 是按某种规则排列的，即对于子集 $S = \{ S_2, S_1 \}$ 来说，$S$ 的状态就是 $[S_1S_2]$。

疑问：P51 这里的 S 规则排列与状态究竟是什么？

疑问：如果 $K_0$ 中不止一个元素怎么办？

解答：这个观察 $\varepsilon \text{-闭包}$ 的定义即可解决。

图 1：子集的构造算法

按：

(2) $M$ 和 $N$ 的输入字母表是相同的，即是 $\Sigma$。
(3) 转换函数 $D$ 是这样定义的。

\[ D([S_1, S_2, ..., S_j], a) = [R_1, R_2, ..., R_j] \]

其中 $(move([S_1, S_2, $ $... S_j], a)) = $ $[R_1, R_2, ..., R_j]$。
(4) $S_0 = $ $\varepsilon \text{-closure}(K_0)$ 为 $M$ 的开始状态。
(5) $S_t = $ $\{ [S_j, S_k,...,S_e] \}$，其中 $[S_j, S_k,...,S_e]$ $\in S$ 且 $\{ S_j, S_k,...,S_e \}$ $\cap \; K_t \neq \varnothing \}$

图 1 是构造 $\text{NFA } N$ 的状态 $K$ 的子集的算法。假定所构造的子集族为 $C$，即 $C = (T_1, T_2,...,T_i)$，其中 $T_1, T_2,...,T_i$ 为状态 $K$ 的子集。

这个概念必须要用具体的例子辅助理解才能够最终掌握，所以，这里就举一个例子：应用上面的算法对下面的图 2 的 $\text{NFA } N$ 构造子集。

图 2

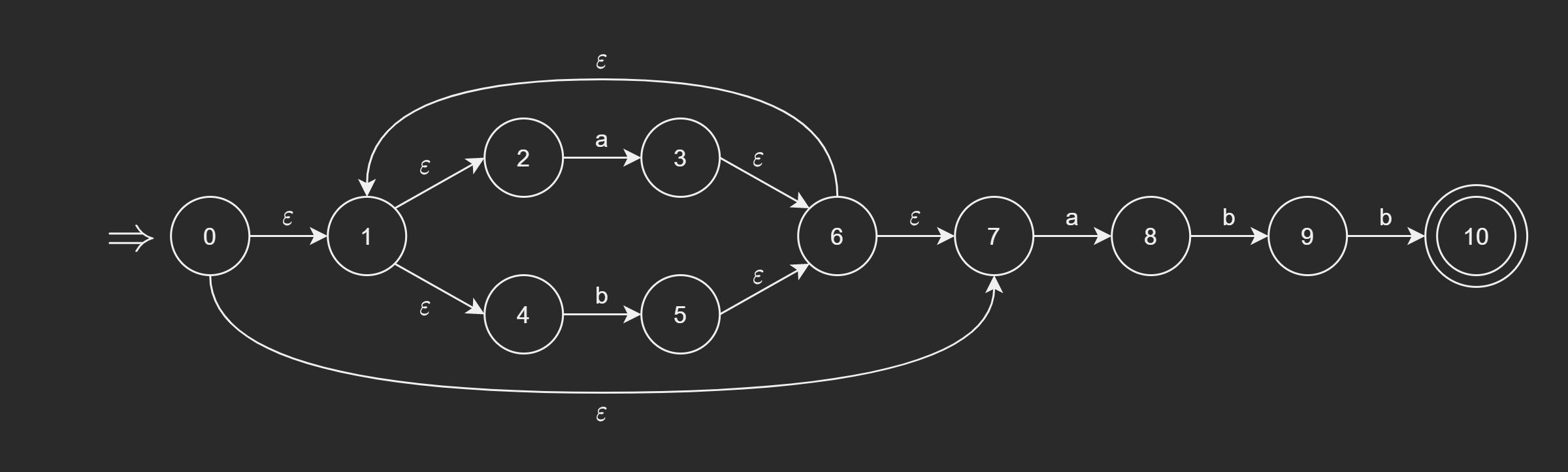
步骤如下：

(1) 首先计算 $\varepsilon \text{-closure(0)}$，令 $T_0 = \varepsilon \text{-closure(0)}$ $=\{0, 1, 2, 4, 7\}$，$T_0$ 未被标记，它现在是子集族 $C$ 的唯一成员。
(2) 标记 $T_0$；计算 $move(T_0, a) = $ $\{ 3, 8 \}$。令 $T_1 = $ $\varepsilon \text{-closure} (move(T_0, a))$ $= \{1, 2, 3, 4, 6, 7, 8\}$，将 $T_1$ 加入 $C$ 中，$T_1$ 未被标记。
计算 $move(T_0, b) = $ $\{ 5 \}$。令 $T_2 = \varepsilon$ $\text{-closure} (move(T_0, b))$ $= \{ 1, 2, 4, 5, 6, 7 \}$，将 $T_2$ 加入 $C$ 中，它未被标记。
(3) 标记 $T_1$；计算 $move(T_1, a) = $ $\{ 3, 8 \}$。计算 $\varepsilon \text{-closure} (move(T_1, a))$，结果为 $\{ 1, 2, 3, 4, 6, 7, 8 \}$，即 $T_1$，$T_1$ 已在 $C$ 中。
计算 $move(T_1, b) = $ $\{ 5, 9 \}$。计算 $\varepsilon \text{-closure} (move(T_1, b))$，结果为 $\{ 1, 2, 4, 5, 6, 7, 9 \}$，令其为 $T_3$，加至 $C$ 中，它未被标记。
(4) （从这里开始，就不单独计算 $move$ 的结果了）标记 $T_2$，计算 $\varepsilon \text{-closure} (move(T_2, a))$，结果为 $\{1, 2, 3, 4, 6, 7, 8\}$，即 $T_1$，$T_1$ 已在 $C$ 中。
计算 $\varepsilon \text{-closure} (move(T_2, b))$，结果为 $\{1, 2, 4, 5, 6, 7\}$，即 $T_2$，$T_2$ 已在 $C$ 中。
(5) 标记 $T_3$，计算 $\varepsilon \text{-closure} (move(T_3, a))$，结果为 $\{1, 2, 3, 4, 6, 7, 8\}$，即 $T_1$。
计算 $\varepsilon \text{-closure} (move(T_3, b))$，结果为 $\{1, 2, 4, 5, 6, 7, 10\}$，令其为 $T_4$，加入 $C$ 中，$T_4$ 未被标记。
(6) 标记 $T_4$，计算 $\varepsilon \text{-closure} (move(T_4, a))$，结果为 $\{1, 2, 3, 4, 6, 7, 8\}$，即 T_1$$。
计算 $\varepsilon \text{-closure} (move(T_4, b))$，结果为 $\{1, 2, 4, 5, 6, 7\}$，即 $T_2$。
至此，算法终止，共构造了 5 个子集：

\[ \begin{split} T_0 &= \{0, 1, 2, 4, 7\} \\ T_1 &= \{1, 2, 3, 4, 6, 7, 8\} \\ T_2 &= \{ 1, 2, 4, 5, 6, 7 \} \\ T_3 &= \{ 1, 2, 4, 5, 6, 7, 9 \} \\ T_4 &= \{1, 2, 4, 5, 6, 7, 10\} \end{split} \]

那么，图 2 的 $\text{NFA } N$ 构造的 $\text{DFA } M$ 如下：

\[ \begin{split} (1)\; &S = \{[T_0], [T_1], [T_2], [T_3], [T_4]\} \\ (2)\; &\Sigma = \{a, b\} \\ (3)\; &D([T_0], a) = [T_1] \\ \; &D([T_0], b) = [T_2] \\ \; &D([T_1], a) = [T_1] \\ \; &D([T_1], b) = [T_3] \\ \; &D([T_2], a) = [T_1] \\ \; &D([T_2], b) = [T_2] \\ \; &D([T_3], a) = [T_1] \\ \; &D([T_3], b) = [T_4] \\ \; &D([T_4], a) = [T_1] \\ \; &D([T_4], b) = [T_2] \\ (4)\; &S_0 = [T_0] \\ (5)\; &S_t = [T_4] \end{split} \]

何为有穷自动机的无用状态？

所谓有穷自动机的无用状态，是指这样的状态：从该自动机的开始状态出发，任何输入串也不能到达的那个状态，或者从这个状态没有通路到达终态。

在有穷自动机中，两个状态 $s$ 和 $t$ 等价的条件？

一致性条件——状态 $s$ 和 $t$ 必须同时为可接受状态（终态）或不可接受状态（非终态）。
蔓延性条件——对于所有输入符号，状态 $s$ 和状态 $t$ 必须转换到等价的状态里。

正规式和有穷自动机的等价性如何说明？

可由以下两点说明：

对于 $\Sigma$ 上的 $\textrm{NFA M}$，可以构造一个 $\Sigma$ 上的正规式，使得 $L(r) = L(M)$。
对于 $\Sigma$ 上的每个正规式 $r$，可以构造一个 $\Sigma$ 上的 $\textrm{NFA M}$，使得 $L(M) = L(r)$。

如何为 $\Sigma$ 上的 $\textrm{NFA M}$ 构造相应的正规式 $r$？

第 1 步，在 $M$ 的状态转换图上加进两个结点，一个为 $x$ 结点，一个为 $y$ 结点。从 $x$ 结点用 $\varepsilon$ 弧连接到 $M$ 的所有初态结点，从 $M$ 的所有终态结点用 $\varepsilon$ 弧连接到 $y$ 结点。形成一个与 $M$ 等价的 $M^{'}$，$M^{'}$ 只有一个初态 $x$ 和一个终态 $y$。
第 2 步，逐步消去 $M^{'}$ 中的所有结点，直至只剩下 $x$ 和 $y$ 结点。在消去的过程中，逐步用正规式来标记弧。其消去的规则如下：

最后 $x$ 和 $y$ 结点间的弧上的标记则为所求的正规式 $r$。

如何从 $\Sigma$ 上的一个正规式 $r$ 构造一个 $\textrm{NFA M}$，使得 $L(M) = L(r)$？

如何从正规文法 $G$ 直接构造一个有穷自动机 $\text{NFA } M$，使得 $L(M) = L(G)$？

(1) $M$ 的字母表与 $G$ 的终结符集相同。
(2) 为 $G$ 中的每个非终结符生成 $M$ 的一个状态（不妨取成相同的名字），$G$ 的开始符 $S$ 是 $M$ 的开始状态 $S$。
(3) 增加一个新状态 $Z$，作为 $M$ 的终态。
(4) 对 $G$ 中的形如 $A \rightarrow tB$ 的规则（其中 $t$ 为终结符或 $\varepsilon$，$A$ 和 $B$ 为非终结符的产生式），构造 $M$ 的一个转换函数 $f(A, t) = B$。
(5) 对 $G$ 中形如 $A \rightarrow t$ 的产生式，构造 $M$ 的一个转换函数 $f(A, t) = Z$。

第四章

何为确定的自顶向下分析方法？

确定的自顶向下分析方法，是从文法的开始符号出发，考虑如何根据当前的输入符号（单词符号）唯一地确定选用哪个产生式替换相应非终结符以往下推导，或如何构造一棵相应的语法树。

如何理解 $\text{FIRST()}$？

设 $G = (V_T, V_N, P, S)$ 是上下文无关文法。

\[ \text{FIRST}(\alpha) = \{a|\alpha \stackrel{*}{\Rightarrow} \alpha \beta, \quad a \in V_T, \alpha, \beta \in V^*\} \]

若 $\alpha \stackrel{*}{\Rightarrow} \epsilon$，则规定 $\epsilon \in \text{FIRST}(\alpha)$。称 $\text{FIRST}(\alpha)$ 为 $\alpha$ 的开始符号集或首符号集。

如何理解 $\text{FOLLOW()}$？

设 $G = (V_T, V_N, P, S)$ 是上下文无关文法，$A \in V_N$，$S$ 是开始符号。

\[ \text{FOLLOW}(A) = \{a|S \stackrel{*}{\Rightarrow} \mu A \beta \; 且 \; a \in V_T, a \in \text{FIRST}(\beta), \mu \in V_T^*, \beta \in V^{+}\} \]

若 $S \stackrel{*}{\Rightarrow} \mu A \beta$，且 $\beta \stackrel{*}{\Rightarrow} \epsilon$，则 $＃ \in \text{FOLLOW}(A)$。

\[ \text{FOLLOW}(A) = \{a|S \stackrel{*}{\Rightarrow} \cdots Aa \cdots, \; a \in V_T\} \]

若有 $S \stackrel{*}{\Rightarrow} \cdots A$，则规定 $＃ \in \text{FOLLOW}(A)$。

这里用 $＃$ 作为输入串的结束符，也称为输入串符号。

因此当文法中含有形如

\[ \begin{split} A \rightarrow \alpha \\ A \rightarrow \beta \end{split} \]

的产生式时，其中 $A \in V_N, \alpha、\beta \in V^*$，若 $\alpha$ 和 $\beta$ 不能同时推导出空，假定 $\alpha \stackrel{*}{\nRightarrow} \epsilon$ $, \beta \stackrel{*}{\Rightarrow} \epsilon$，则当 $\text{FIRST}(\alpha)$ $\cap$ $(\text{FIRST}(\beta)$ $\cup$ $\text{FOLLOW}(A)) = \varnothing$ 时，对于非终结符 $A$ 的替换仍可唯一地确定候选。

如何理解 $\text{SELECT()}$？

给定上下文无关文法的产生式 $A \rightarrow \alpha$ $, $ $A \in V_N, \alpha \in V^*$，

若 $\alpha \stackrel{*}{\nRightarrow} \varepsilon$，则 $\text{SELECT}(A \rightarrow \alpha)$ $=$ $\text{FIRST}(\alpha)$。
若 $\alpha \stackrel{*}{\Rightarrow} \varepsilon$，则 $\text{SELECT}(A \rightarrow \alpha)$ $=$ $(\text{FIRST}(\alpha) - \{\varepsilon\})$ $\cup$ $\text{FOLLOW}(A)$。

何为 $\text{LL}(1)$ 文法？

一个上下文无关文法是 $\text{LL}(1)$ 的充分必要条件是,

对每个非终结符 $A$ 的两个不同产生式，$A \rightarrow \alpha$ $,$ $A \rightarrow \beta$，满足

\[ \text{SELECT}(A \rightarrow \alpha) \cap \text{SELECT}(A \rightarrow \beta) = \varnothing \]

其中 $\alpha、\beta$ 不同时能 $\stackrel{*}{\Rightarrow} \epsilon$。

$\text{LL}(1)$ 的含义是：第 1 个 $\text{L}$ 表明自顶向下分析是从左向右扫描输入串，第 2 个 $\text{L}$ 表明分析过程中将用最左推导，1 表明只需要向右看一个符号便可决定如何推导，即选择哪个产生式（规则）进行推导。

如何判别某文法是否是 $\text{LL}(1)$ 文法？

首先计算 $\text{FIRST}$、$\text{FOLLOW}$、$\text{SELECT}$ 集合，然后根据定义判别文法是否是 $\text{LL}(1)$ 文法。

如何计算一个文法符号 $X \in V$ 的 $\text{FIRST}$ 集 $\text{FIRST}(X)$？

① 若 $X \in V_T$，则 $\text{FIRST}(X) = \{X\}$。
② 若 $X \in V_N$，且有产生式 $X \rightarrow a \cdots$ $,$ $a \in V_T$，则 $a \in \text{FIRST}(X)$。
③ 若 $X \in V_N$，$X \rightarrow \varepsilon$，则 $\varepsilon \in \text{FIRST}(X)$。
④ 若 $X, Y_1, Y_2,$ $\cdots$ $, Y_n \in V_N$，而有产生式 $X \rightarrow Y_1Y_2 \cdots Y_n$。当 $Y_1, Y_2, \cdots, Y_{i - 1}$ $\stackrel{*}{\Rightarrow} \varepsilon$ 时（其中 $1 \leqslant i \leqslant n$），则 $\text{FIRST}(Y_1) - \{\varepsilon\},$ $\text{FIRST}(Y_2) - \{\varepsilon\},$ $\cdots$ $, \text{FIRST}(Y_{i - 1}) - \{\varepsilon\},$ $\text{FIRST}(Y_i)$ 都包含在 $\text{FIRST}(X)$ 中，即

\[ \text{FIRST}(X) = (\text{FIRST}(Y_1) \cup \text{FIRST}(Y_2) \cdots \cup \text{FIRST}(Y_i)) - \{\varepsilon\} \]

⑤ 当 ④ 中所有 $Y_i \stackrel{*}{\Rightarrow} \varepsilon$ $,$ $(i = 1, 2, \cdots, n)$，则

\[ \text{FIRST}(X) = (\text{FIRST}(Y_1) \cup \text{FIRST}(Y_2) \cdots \cup \text{FIRST}(Y_n)) \cup \{\varepsilon\} \]

反复使用上述 ②~⑤ 步，直到每个符号的 $\text{FIRST}$ 集合不再增大为止。

如何计算一个符号串的 $\text{FIRST}$ 集合？

若符号串 $\alpha \in V^*$ $,$ $\alpha = X_1 X_2 \cdots X_n$，当 $X_1$ 不能 $\stackrel{*}{\Rightarrow} \varepsilon$，则置 $\text{FIRST}(\alpha) = \text{FIRST}(X_1)$。

若对任何 $j(1 \leqslant j \leqslant i - 1,$ $2 \leqslant i \leqslant n)$ $,$ $\varepsilon \in \text{FIRST}(X_j)$ $,$ $\varepsilon \notin \text{FIRST}(X_i)$，则

\[ \text{FIRST}(\alpha) = \bigcup_{j = 1}^{i - 1}(\text{FIRST}(X_j) - \{\varepsilon\}) \cup \text{FIRST}(X_i) \]

当对任何 $j(1 \leqslant j \leqslant n)$，$\text{FIRST}(X_j)$ 都含有 $\varepsilon$ 时，则

\[ \text{FIRST}(\alpha) = \bigcup_{j = 1}^{n}(\text{FIRST}(X_j) - \{\varepsilon\}) \cup \{\varepsilon\} \]

按：这里最后一个公式书上的写法似乎有点问题。

如何计算 $\text{FOLLOW}$ 集？

对文法中的每一个 $A \in V_N$，根据定义计算 $\text{FOLLOW}(A)$。

① 设 $S$ 为文法的开始符号，把 $\{＃\}$ 加入 $\text{FOLLOW}(S)$ 中（这里＃为句子括号）。

按：＃似为句子结束符号。

② 若 $A \rightarrow \alpha B \beta$ 是一个产生式，则把 $\text{FIRST}(\beta)$ 的非空元素加入 $\text{FOLLOW}(B)$ 中。
如果 $\beta \stackrel{*}{\Rightarrow} \varepsilon$，则把 $\text{FOLLOW}(A)$ 也加入 $\text{FOLLOW}(B)$ 中，因为当有形如

\[ \begin{split} D &\rightarrow \alpha_{1} A \beta_{1} \\ A &\rightarrow \alpha B \beta \end{split} \]

的产生式时，$A, B, D \in V_N$，$\alpha, \alpha_{1}, \beta, \beta_{1} \in V^*$，在推导过程中可能出现如下的句型序列：

\[ S \stackrel{*}{\Rightarrow} \cdots \alpha_{1} A \beta_{1} \cdots \Rightarrow \alpha_{1} \alpha B \beta \beta{1} \cdots \Rightarrow \cdots \alpha_{1} \alpha B \beta_{1} \cdots \]

因此，有 $\text{FOLLOW}(A)$ $\subseteq$ $\text{FOLLOW}(B)$。

③ 反复使用 ② 直到每个非终结符的 $\text{FOLLOW}$ 集不再增大为止。

如何计算某一文法中的每一个产生式的 $\text{SELECT}$ 集？

直接根据定义来判断：

给定上下文无关文法的产生式 $A \rightarrow \alpha$ $, $ $A \in V_N, \alpha \in V^*$，

若 $\alpha \stackrel{*}{\nRightarrow} \varepsilon$，则 $\text{SELECT}(A \rightarrow \alpha)$ $=$ $\text{FIRST}(\alpha)$。
若 $\alpha \stackrel{*}{\Rightarrow} \varepsilon$，则 $\text{SELECT}(A \rightarrow \alpha)$ $=$ $(\text{FIRST}(\alpha) - \{\varepsilon\})$ $\cup$ $\text{FOLLOW}(A)$。