《编译原理第三版》（张素琴）第三章学习札记

何为正规文法？

这个概念在第二章有讲过，这里再次摘录一下。

正规文法也称为 3 型文法 \(G = (V_N, V_T, S, P)\)，其 \(P\) 中的每一条规则都有下述形式：\(A \rightarrow aB\) 或 \(A \rightarrow a\)，其中 \(A, B \in V_N, \; a \in V_T^*\)。

正规文法所描述的是 \(V_T\) 上的正规集。

何为正规集？

按：本书中似乎没有正规集的概念。遂从《编译原理 第二版》黑书摘录其定义如下

可以用一个正则表达式定义的语言叫做正则集合（regular set）。

黑书中的翻译是“正则集合”，其实和“正规集”是一个意思。

结合老师所讲，所谓正规集，可以和前面第二章的语言（\(L(G)\)）这一概念结合来看，它们表达的东西其实是很类似的，因此，正规集所表达的意思就是正规式（正则表达式）所产生的所有字串的集合。

何为正规式？

正规式也称正则表达式，是表示正规集的工具。

(1). \(\varepsilon\) 和 \(\varnothing\) 都是 \(\Sigma\) 上的正规式，它们所表示的正规集分别为 \(\{ \varepsilon \}\) 和 \(\varnothing\)。
(2). 任何 \(a \in \Sigma\)，\(a\) 是 \(\Sigma\) 上的一个正规式，它所表示的正规集为 \(\{ a \}\)。
(3). 假定 \(e_1\) 和 \(e_2\) 都是 \(\Sigma\) 上的正规式，它们所表示的正规集分别为 \(L(e_1)\) 和 \(L(e_2)\)，那么，\((e_1)\)、\(e_1|e_2\)、\(e_1 \cdot e_2\) 和 \(e_1^*\) 也都是正规式，它们所表示的正规集分别为 \(L(e_1)\)、\(L(e_1) \cup L(e_2)\)、\(L(e_1)L(e_2)\) 和 \((L(e_1))^*\)。
(4). 仅由有限次使用上述 3 个步骤而定义的表达式才是 \(\Sigma\) 上的正规式，仅由这些正规式所表示的符号串的集合才是 \(\Sigma\) 上的正规集。

其中的 \(|\) 读为“或”；\(\cdot\) 读为“连接”；\(*\) 读为“闭包”。在不致混淆时，括号可省去，但规定算符的优先顺序为先 \(*\)，再 \(\cdot\)，最后 \(|\)。连接符 \(\cdot\) 一般可省略不写。\(*\)、\(\cdot\)、和 \(|\) 都是左结合的。

正规文法转正规式的 3 条规则？

1. 正规式：\(A \rightarrow xy\)

   正规文法：

   \[ \begin{split} A &\rightarrow xB \\ B &\rightarrow y \end{split} \]

2. 正规式：\(A \rightarrow x^*y\)

   正规文法：

   \[ \begin{split} A &\rightarrow xB \\ A &\rightarrow y \\ B &\rightarrow xB \\ B &\rightarrow y \end{split} \]

3. 正规式：\(A \rightarrow x|y\)

   正规文法：

   \[ \begin{split} A &\rightarrow x \\ A &\rightarrow y \end{split} \]

课堂小问：

\[ A \rightarrow xA \\ A \rightarrow y \]

\(x\) 可能是多个 \(*\) 闭包的组合。

疑问 P45？

(1). 例 3.3，表示无符号数的正规式似乎有点问题。

可以利用 \(\varepsilon A = A\) 来理解。那么，这个式子就是对的。

P45 \((a|b)^* = (a^* b^*)^*\) 如何理解？

可以将 \((a|b)^*\) 展开成类似 \((a|b)(a|b) \cdots (a|b)\) 的形式，然后每一个括号内可以随便是 \(a\) 或 \(b\)。

正规式的代数规律？

\[ \begin{split} &(1) \; r|s = s|r \\ &(2) \; r|(s|t) = (r|s)|t \\ &(3) \; (rs)t = r(st) \\ &(4) \; r(s|t) = rs|rt, \; (s|t)r = sr|tr \\ &(5) \; \varepsilon r = r, \; r\varepsilon = r \\ &(6) \; r|r = r \end{split} \]

将正规文法转换成正规式的 3 条规则？

1. 规则一：

   \[ \begin{split} 文法产生式：&A \rightarrow xB \quad B \rightarrow y \\ 正规式：&A = xy \end{split} \]

2. 规则二：

   \[ \begin{split} 文法产生式：&A \rightarrow xA|y \\ 正规式：&A = x^*y \end{split} \]

3. 文法产生式：

   \[ \begin{split} 文法产生式：&A \rightarrow x \quad A \rightarrow y \\ 正规式：&A = x|y \end{split} \]

何为确定的有穷自动机（\(\textrm{DFA}\)）？

一个确定的有穷自动机 \(M\) 是一个五元组：

\[ M = (K, \Sigma, f, S, Z) \]

其中：

(1) \(K\) 是一个有穷集，它的每一个元素称为一个状态。
(2) \(\Sigma\) 是一个有穷字母表，它的每一个元素称为一个输入符号，所以也称 \(\Sigma\) 为输入符号表。
(3) \(f\) 是转换函数，是 \(K \times \Sigma \rightarrow K\) 上的映像。例如，\(f(k_i, a) = k_j\) \((k_i \in K, k_j \in K, a \in \Sigma)\) 就意味着，当前状态为 \(k\)、输入字符为 \(a\) 时，将转换到下一状态 \(k_j\)，把 \(k_j\) 称作 \(k_i\) 的一个后继状态。
(4) \(S \in K\)，是唯一的一个初态。
(5) \(Z \subseteq K\)，是一个终态集，终态也称可接受或结束状态。

一个 \(DFA\) 可以表示成一个状态图（或称状态转换图）。假定 \(DFA \; M\) 含有 \(m\) 个状态，\(n\) 个输入符号，那么这个状态图含有 \(m\) 个节点，每个节点最多有 \(n\) 个弧射出，整个图含有唯一一个初态节点和若干个终态节点，初态节点冠以“\(\Rightarrow\)”或标以“\(-\)”，终态节点终态节点用双圈表示或标以“\(+\)”，若 \(f(k_i, a) = k_j\)，则从状态节点 \(k_i\) 到状态节点 \(k_j\) 画标记为 \(a\) 的弧。

对于 \(\Sigma^*\) 中的任何符号串，若存在一条从初态节点到某一终态节点的道路，且这条路上所有弧的标记连接成的符号串等于 \(t\)，则称 \(t\) 可为 \(DFA \; M\) 所接受，若 \(M\) 的初态节点同时又是终态节点，则空字可为 \(M\) 所识别（接受）。
可换一种方式叙述如下：
若 $t ^*, $ \(f(S, t) = P\)，其中 \(S\) 为 \(\textrm{DFA M}\) 的开始状态， \(P \in Z\)，\(Z\) 为终态集。则称 \(t\) 可为 \(\textrm{DFA M}\) 所接受（识别）。

何为不确定的有穷自动机（\(\textrm{NFA}\)）？

一个不确定的有穷自动机 \(M\) 是一个五元组：

\[ M = (K, \Sigma, f, S, Z) \]

其中：

(1) \(K\) 是一个有穷集，它的每个元素称为一个状态。
(2) \(\Sigma\) 是一个有穷字母表，它的每个元素称为一个输入符号。
(3) \(f\) 是一个从 \(K \times \Sigma^*\) 到 \(K\) 的全体子集的映像，即 \(K \times \Sigma^* \rightarrow 2^K\)，其中 \(2^K\) 表示 \(K\) 的幂集。
(4) \(S \subseteq K\)，是一个非空初态集。
(5) \(Z \subseteq K\)，是一个终态集。

一个含有 \(m\) 个状态和 \(n\) 个输入符号的 \(\textrm{NFA}\) 可表示成一张状态转换图，这张图含有 \(m\) 个状态结点，每个结点可射出若干条箭弧与别的节点相连接，每条弧用 \(\Sigma^*\) 中的一个串作标记，整个图至少含有一个初态结点以及若干个终态结点。

何为状态集合 \(I\) 的 \(\varepsilon\text{-闭包}\)？

状态集合 \(I\) 的 \(\varepsilon\text{-闭包}\)，表示为 \(\varepsilon \text{-closure(I)}\)，定义为一个状态集，是状态集 \(I\) 中任何状态 \(S\) 经任意条 \(\varepsilon\) 弧能到达的状态的集合。

何为状态集合 \(I\) 的 \(a\) 弧转换？

状态集合 \(I\) 的 \(a\) 弧转换，表示为 \(move(I, a)\)，定义为状态集合 \(J\)，其中 \(J\) 是所有哪些可从 \(I\) 中的某一状态经过一条 \(a\) 弧而到达的状态的全体。

如何将一个 \(\textrm{NFA}\) 转换为等价的 \(\textrm{DFA}\)？

这里介绍的方法就是子集法。

假设 \(\textrm{NFA N} =\) \(\{K, \Sigma, f, K_0, K_t\}\) 按照如下方法构造一个 \(\textrm{DFA M} =\) \((S, \Sigma, D, S_0, S_t)\) 使得 \(L(M) = L(N)\)：

(1) \(M\) 的状态集 \(S\) 由 \(K\) 的一些子集（构造 \(K\) 的子集见下图）组成。用 \([S_1, S_2, ..., S_j]\) 表示 \(S\) 的元素，其中 \(S_1, S_2, ..., S_j\) 是 \(K\) 的状态。并且约定，状态 \(S_1, S_2, ..., S_j\) 是按某种规则排列的，即对于子集 \(S = \{ S_2, S_1 \}\) 来说，\(S\) 的状态就是 \([S_1S_2]\)。

疑问：P51 这里的 S 规则排列与状态究竟是什么？

疑问：如果 \(K_0\) 中不止一个元素怎么办？

解答：这个观察 \(\varepsilon \text{-闭包}\) 的定义即可解决。

按：

(2) \(M\) 和 \(N\) 的输入字母表是相同的，即是 \(\Sigma\)。
(3) 转换函数 \(D\) 是这样定义的。

\[ D([S_1, S_2, ..., S_j], a) = [R_1, R_2, ..., R_j] \]

其中 $(move([S_1, S_2, $ $... S_j], a)) = $ \([R_1, R_2, ..., R_j]\)。
(4) $S_0 = $ \(\varepsilon \text{-closure}(K_0)\) 为 \(M\) 的开始状态。
(5) $S_t = $ \(\{ [S_j, S_k,...,S_e] \}\)，其中 \([S_j, S_k,...,S_e]\) \(\in S\) 且 \(\{ S_j, S_k,...,S_e \}\) \(\cap \; K_t \neq \varnothing \}\)

图 1 是构造 \(\text{NFA } N\) 的状态 \(K\) 的子集的算法。假定所构造的子集族为 \(C\)，即 \(C = (T_1, T_2,...,T_i)\)，其中 \(T_1, T_2,...,T_i\) 为状态 \(K\) 的子集。

这个概念必须要用具体的例子辅助理解才能够最终掌握，所以，这里就举一个例子：应用上面的算法对下面的图 2 的 \(\text{NFA } N\) 构造子集。

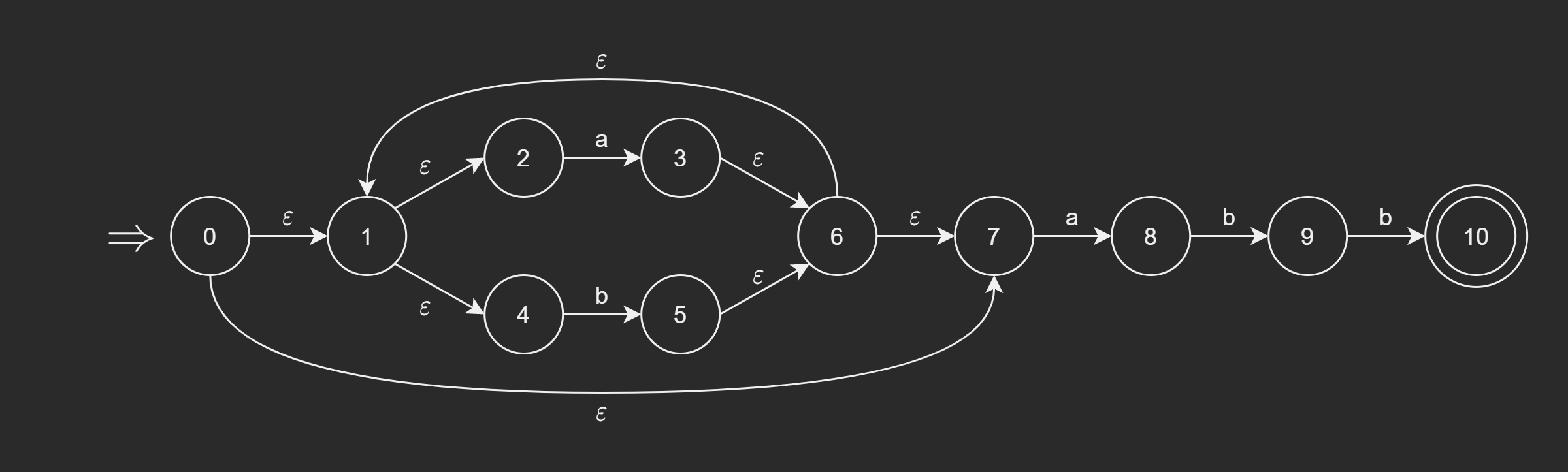
步骤如下：

(1) 首先计算 \(\varepsilon \text{-closure(0)}\)，令 \(T_0 = \varepsilon \text{-closure(0)}\) \(=\{0, 1, 2, 4, 7\}\)，\(T_0\) 未被标记，它现在是子集族 \(C\) 的唯一成员。
(2) 标记 \(T_0\)；计算 $move(T_0, a) = $ \(\{ 3, 8 \}\)。令 $T_1 = $ \(\varepsilon \text{-closure} (move(T_0, a))\) \(= \{1, 2, 3, 4, 6, 7, 8\}\)，将 \(T_1\) 加入 \(C\) 中，\(T_1\) 未被标记。
计算 $move(T_0, b) = $ \(\{ 5 \}\)。令 \(T_2 = \varepsilon\) \(\text{-closure} (move(T_0, b))\) \(= \{ 1, 2, 4, 5, 6, 7 \}\)，将 \(T_2\) 加入 \(C\) 中，它未被标记。
(3) 标记 \(T_1\)；计算 $move(T_1, a) = $ \(\{ 3, 8 \}\)。计算 \(\varepsilon \text{-closure} (move(T_1, a))\)，结果为 \(\{ 1, 2, 3, 4, 6, 7, 8 \}\)，即 \(T_1\)，\(T_1\) 已在 \(C\) 中。
计算 $move(T_1, b) = $ \(\{ 5, 9 \}\)。 计算 \(\varepsilon \text{-closure} (move(T_1, b))\)，结果为 \(\{ 1, 2, 4, 5, 6, 7, 9 \}\)，令其为 \(T_3\)，加至 \(C\) 中，它未被标记。
(4) （从这里开始，就不单独计算 \(move\) 的结果了）标记 \(T_2\)，计算 \(\varepsilon \text{-closure} (move(T_2, a))\)，结果为 \(\{1, 2, 3, 4, 6, 7, 8\}\)，即 \(T_1\)，\(T_1\) 已在 \(C\) 中。
计算 \(\varepsilon \text{-closure} (move(T_2, b))\)，结果为 \(\{1, 2, 4, 5, 6, 7\}\)，即 \(T_2\)，\(T_2\) 已在 \(C\) 中。
(5) 标记 \(T_3\)，计算 \(\varepsilon \text{-closure} (move(T_3, a))\)，结果为 \(\{1, 2, 3, 4, 6, 7, 8\}\)，即 \(T_1\)。
计算 \(\varepsilon \text{-closure} (move(T_3, b))\)，结果为 \(\{1, 2, 4, 5, 6, 7, 10\}\)，令其为 \(T_4\)，加入 \(C\) 中，\(T_4\) 未被标记。
(6) 标记 \(T_4\)，计算 \(\varepsilon \text{-closure} (move(T_4, a))\)，结果为 \(\{1, 2, 3, 4, 6, 7, 8\}\)，即 T_1$$。
计算 \(\varepsilon \text{-closure} (move(T_4, b))\)，结果为 \(\{1, 2, 4, 5, 6, 7\}\)，即 \(T_2\)。
至此，算法终止，共构造了 5 个子集：

\[ \begin{split} T_0 &= \{0, 1, 2, 4, 7\} \\ T_1 &= \{1, 2, 3, 4, 6, 7, 8\} \\ T_2 &= \{ 1, 2, 4, 5, 6, 7 \} \\ T_3 &= \{ 1, 2, 4, 5, 6, 7, 9 \} \\ T_4 &= \{1, 2, 4, 5, 6, 7, 10\} \end{split} \]

那么，图 2 的 \(\text{NFA } N\) 构造的 \(\text{DFA } M\) 如下：

\[ \begin{split} (1)\; &S = \{[T_0], [T_1], [T_2], [T_3], [T_4]\} \\ (2)\; &\Sigma = \{a, b\} \\ (3)\; &D([T_0], a) = [T_1] \\ \; &D([T_0], b) = [T_2] \\ \; &D([T_1], a) = [T_1] \\ \; &D([T_1], b) = [T_3] \\ \; &D([T_2], a) = [T_1] \\ \; &D([T_2], b) = [T_2] \\ \; &D([T_3], a) = [T_1] \\ \; &D([T_3], b) = [T_4] \\ \; &D([T_4], a) = [T_1] \\ \; &D([T_4], b) = [T_2] \\ (4)\; &S_0 = [T_0] \\ (5)\; &S_t = [T_4] \end{split} \]

何为有穷自动机的无用状态？

所谓有穷自动机的无用状态，是指这样的状态：从该自动机的开始状态出发，任何输入串也不能到达的那个状态，或者从这个状态没有通路到达终态。

在有穷自动机中，两个状态 \(s\) 和 \(t\) 等价的条件？

• 一致性条件——状态 \(s\) 和 \(t\) 必须同时为可接受状态（终态）或不可接受状态（非终态）。
• 蔓延性条件——对于所有输入符号，状态 \(s\) 和状态 \(t\) 必须转换到等价的状态里。

正规式和有穷自动机的等价性如何说明？

可由以下两点说明：

• 对于 \(\Sigma\) 上的 \(\textrm{NFA M}\)，可以构造一个 \(\Sigma\) 上的正规式，使得 \(L(r) = L(M)\)。
• 对于 \(\Sigma\) 上的每个正规式 \(r\)，可以构造一个 \(\Sigma\) 上的 \(\textrm{NFA M}\)，使得 \(L(M) = L(r)\)。

如何为 \(\Sigma\) 上的 \(\textrm{NFA M}\) 构造相应的正规式 \(r\)？

第 1 步，在 \(M\) 的状态转换图上加进两个结点，一个为 \(x\) 结点，一个为 \(y\) 结点。从 \(x\) 结点用 \(\varepsilon\) 弧连接到 \(M\) 的所有初态结点，从 \(M\) 的所有终态结点用 \(\varepsilon\) 弧连接到 \(y\) 结点。形成一个与 \(M\) 等价的 \(M^{'}\)，\(M^{'}\) 只有一个初态 \(x\) 和一个终态 \(y\)。
第 2 步，逐步消去 \(M^{'}\) 中的所有结点，直至只剩下 \(x\) 和 \(y\) 结点。在消去的过程中，逐步用正规式来标记弧。其消去的规则如下：

最后 \(x\) 和 \(y\) 结点间的弧上的标记则为所求的正规式 \(r\)。

如何从 \(\Sigma\) 上的一个正规式 \(r\) 构造一个 \(\textrm{NFA M}\)，使得 \(L(M) = L(r)\)？

如何从正规文法 \(G\) 直接构造一个有穷自动机 \(\text{NFA } M\)，使得 \(L(M) = L(G)\)？

(1) \(M\) 的字母表与 \(G\) 的终结符集相同。
(2) 为 \(G\) 中的每个非终结符生成 \(M\) 的一个状态（不妨取成相同的名字），\(G\) 的开始符 \(S\) 是 \(M\) 的开始状态 \(S\)。
(3) 增加一个新状态 \(Z\)，作为 \(M\) 的终态。
(4) 对 \(G\) 中的形如 \(A \rightarrow tB\) 的规则（其中 \(t\) 为终结符或 \(\varepsilon\)，\(A\) 和 \(B\) 为非终结符的产生式），构造 \(M\) 的一个转换函数 \(f(A, t) = B\)。
(5) 对 \(G\) 中形如 \(A \rightarrow t\) 的产生式，构造 \(M\) 的一个转换函数 \(f(A, t) = Z\)。