浮点数与 IEEE754 标准浮点数

浮点表示是对形如 \(V = x \times 2^y\) 的有理数进行编码。

1. 二进制小数

考虑一个形如

\[ b_mb_{m - 1} \cdots b_1b_0.b_{-1}b_{-2} \cdots b_{-n - 1}b_{-n} \]

的表示法，其中每个二进制数字，或者称为位，\(b_i\) 的取值是 0 或 1，如下图所示。

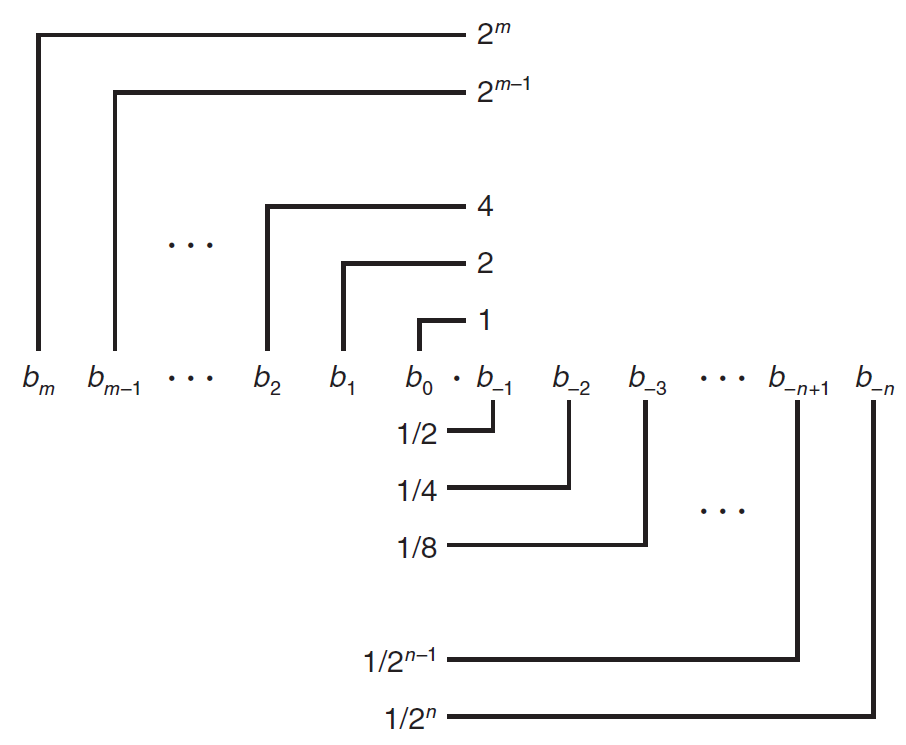
这种表示方法表示的数 \(b\) 定义如下：

\[ b = \sum_{i = -n}^{m} 2^i \times b_i \]

计算举例：

\[ 101.11_2 = 1 \times 2^2 + 0 \times 2^1 + 1 \times 2^0 + 1 \times 2^{-1} + 1 \times 2^{-2} = 5 \frac{3}{4} \]

注意，形如 \(0.11 \cdots 1_2\) 的数表示的是刚好小于 1 的数。例如，\(0.111111_2\) 表示 \(\frac{63}{64}\)，我们用简单的表达法 \(1.0 - \varepsilon\) 来表示这样的数值。

按：\(\varepsilon\) 这个是我们的老朋友了，在物理实验或者计算方法这些课程中，学习误差的表达时经常会见到。

假定我们仅考虑有限长度的编码，那么十进制表示法不能准确地表达像 \(\frac{1}{3}\) 和 \(\frac{5}{7}\) 这样的数。类似，小数的二进制表示法只能表示哪些能够被写成 \(x \times 2^y\) 的数。其他的值只能够被近似地表示。例如，数字 \(\frac{1}{5}\) 可以用十进制小数 \(0.20\) 精确表示。不过，我们并不能把它准确地表示为一个二进制小数，我们只能近似地表示它，增加二进制表示的长度可以提高表示的精度。

2. IEEE 浮点数表示

IEEE 浮点数即采用 IEEE754 标准来表示的浮点数。

IEEE 浮点标准用 \(V = (-1)^s \times M \times 2^E\) 的形式来表示一个数：

• 符号（sign）\(s\) 决定这个数是负数（\(s = 1\)）还是正数（\(s = 0\)），而对于数值 0 的符号位解释作为特殊情况处理（后面有讲，即非规格数相关）。
• 尾数（significand）\(M\) 是一个二进制小数，它的范围是 \(1 \sim 2 - \epsilon\)，或者是 \(0 \sim 1 - \varepsilon\)。
• 阶码（exponent）\(E\) 的作用是对浮点数加权，这个权重是 2 的 \(E\) 次幂（可能是负数）。
  按：这里的“权重是 2 的 \(E\) 次幂”并不是指 \(E\) 是 2 的幂，而是指 \(2^E\) 是 2 的幂。

将浮点数的位表示划分成三个字段，分别对这些值进行编码：

• 一个单独的符号位 \(s\) 直接编码符号 \(s\)。
• \(k\) 位的阶码字段 \(exp = e_{k - 1} \cdots e_1e_0\) 编码阶码 \(E\)。
• \(n\) 位小数字段 \(frac = f_{n -1} \cdots f_1f_0\) 编码尾数 \(M\)，但是编码出来的值也依赖阶码字段的值是否等于 0（这个涉及到规格数和非规格数，具体见下面的讲解）。

在单精度浮点格式（C 语言中的 float）中，\(s\)、\(exp\) 和 \(frac\) 字段分别为 1 位、\(k = 8\) 位和 \(n = 23\) 位，得到一个 32 位的表示。
在双精度浮点格式（C 语言中的 double）中，\(s\)、\(exp\) 和 \(frac\) 字段分别为 1 位、\(k = 11\) 位和 \(n = 52\) 位，得到一个 64 位的表示。

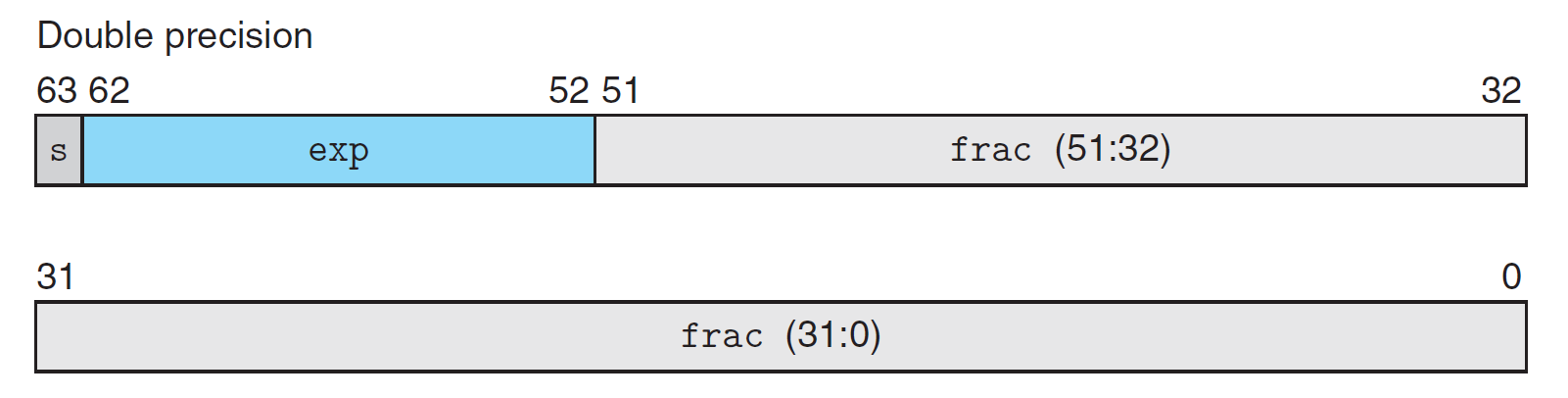
给定位的表示，根据 \(exp\) 的值，被编码的值可以分成三种不同的情况（第三种情况有两个变种）。

举例，单精度格式的情况：

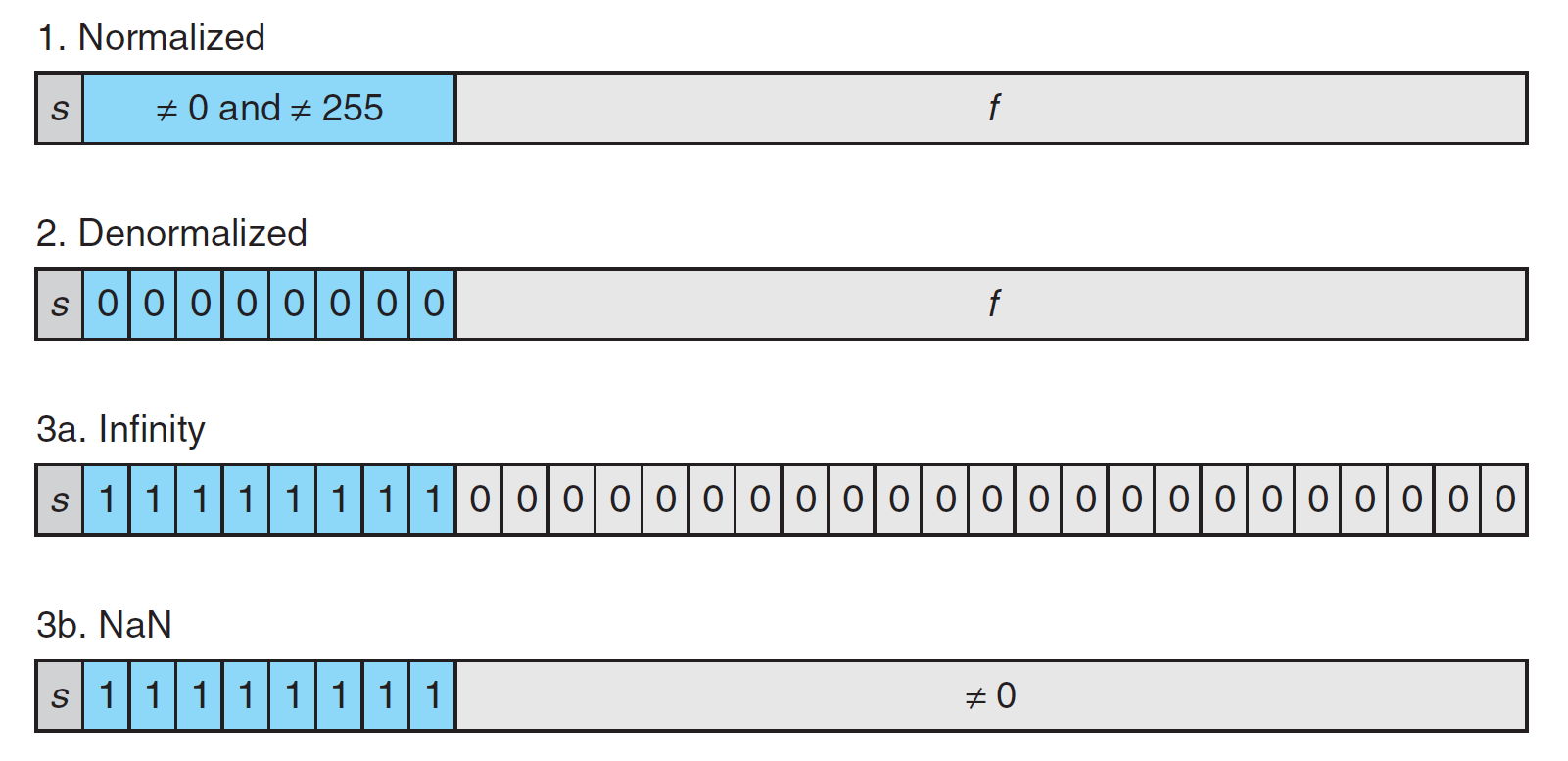
情况 1；规格化的值

当 \(exp\) 的所有位既不全为 0（即 \(exp\) 数值为 0），也不全为 1（单精度数值为 255，双精度数值为 2047），都属于这类情况。在这种情况下，阶码字段被解释为以偏置值（biased）形式表示的有符号整数。也就是说，阶码的值是 \(E = e - Bias\)（\(e\) 即 \(exp\)），其中 \(e\) 是无符号数，其位表示为 \(e_{k - 1} \cdots e_1e_0\)，而 \(Bias\) 是一个等于 \(2^{k - 1} - 1\)（单精度是 127，双精度是 1023）的偏置值。由此产生指数的取值范围，对于单精度是 \(-126 \sim +127\)，而对于双精度是 \(-1022 \sim +1023\)。

按：这里说的指数范围，就拿单精度的范围 \(-126 \sim +127\)，因为单精度阶码一共有 8 位，所以 \(e\) 的范围是 \(0 \sim 255\)，然后根据 \(E = e - Bias\)、\(Bias = 127\) 来算，得到的指数 \(E\) 的取值范围是 \(-127 \sim +128\)，但是，别忘了 \(e\) 还要去掉 0 和 255 两个值，然后再算，就得到了 \(-126 \sim +127\)。

小数字段 \(frac\) 被解释为描述小数值 \(f\)，其中 \(0 \leqslant f < 1\)，其二进制表示为 \(0.f_{n - 1} \cdots f_1f_0\)，也就是二进制小数点在最高有效位的左边。尾数定义为 \(M = 1 + f\)。有时，这种方式也叫做隐含的以 1 开头的（implied leading 1）表示，因为我们可以把 \(M\) 看成一个二进制表达式为 \(1.f_{n - 1}f_{n - 2} \cdots f_0\) 的数字。因为我们是可以通过调整阶码 \(E\)，使得尾数 \(M\) 在范围 \(1 \leqslant M < 2\) 之中（假设没有溢出），所以这种表达方式的好处是可以轻松获得一个额外的精度位。因为第一位总是等于 1，那么我们就不需要显式地表示它。

情况 2：非规格化的值

当阶码域为全 0 时，所表示的数是非规格化形式。在这种情况下，阶码值是 \(E = 1 - Bias\)，而尾数的值是 \(M = f\)，也就是小数字段的值，不包含隐含的开头的 1。

按：这里要仔细注意。

非规格化数有两个用途。首先，它们提供了一种表示数值 0 的方法，因为使用规格化数，我们必须要使 \(M \geqslant 1\)，因此我们就不能表示 0。实际上，\(+0.0\) 的浮点表示的位模式为全 0：符号位是 0，阶码字段全为 0（表明是一个非规格化值），而小数域也全为 0，这就得到了 \(M = f = 0\)。令人奇怪的是，当符号位为 1，而其他域全为 0 时，我们得到值 \(-0.0\)。根据 IEEE 的浮点格式，值 \(+0.0\) 和 \(-0.0\) 在某些方面被认为是不同的，而在其他方面是相同的。

非规格化数的另外一个功能是表示哪些非常接近于 \(0.0\) 的数。它们提供了一种属性，称为逐渐溢出（gradual underflow），其中，可能的数值分布均匀地接近于 \(0.0\)。

按：这里的逐渐溢出表示的大概是从非规格数平滑地溢出，然后就到了规格数（可以参考之后的表格示例）。

情况 3：特殊值

最后一类数值是指阶码全为 1 的时候出现的值。

• 当小数域全为 0 时，得到的值表示无穷，当 \(s = 0\) 时是 \(+\infty\)，或者当 \(s = 1\) 时是 \(-\infty\)。当我们把两个非常大的数相乘，或者除以零时，无穷能够表示溢出的结果。
• 当小数域为非零时，结果值被称为“\(NaN\)”，即“不是一个数（Not a Number）”的缩写。一些运算的结果不能是实数或无穷，就会返回这样的 \(NaN\) 值，比如当计算 \(\sqrt{-1}\) 或 \(\infty - \infty\) 时。在某些应用中，表示未初始化的数据时，它们也很有用处。

3. 数字示例

下图的表格是 8 位浮点格式的非负值示例。由于阶码位 \(k = 4\)，小数位 \(n = 3\)，所以偏置量是 \(2^{4 - 1} - 1 = 7\)。

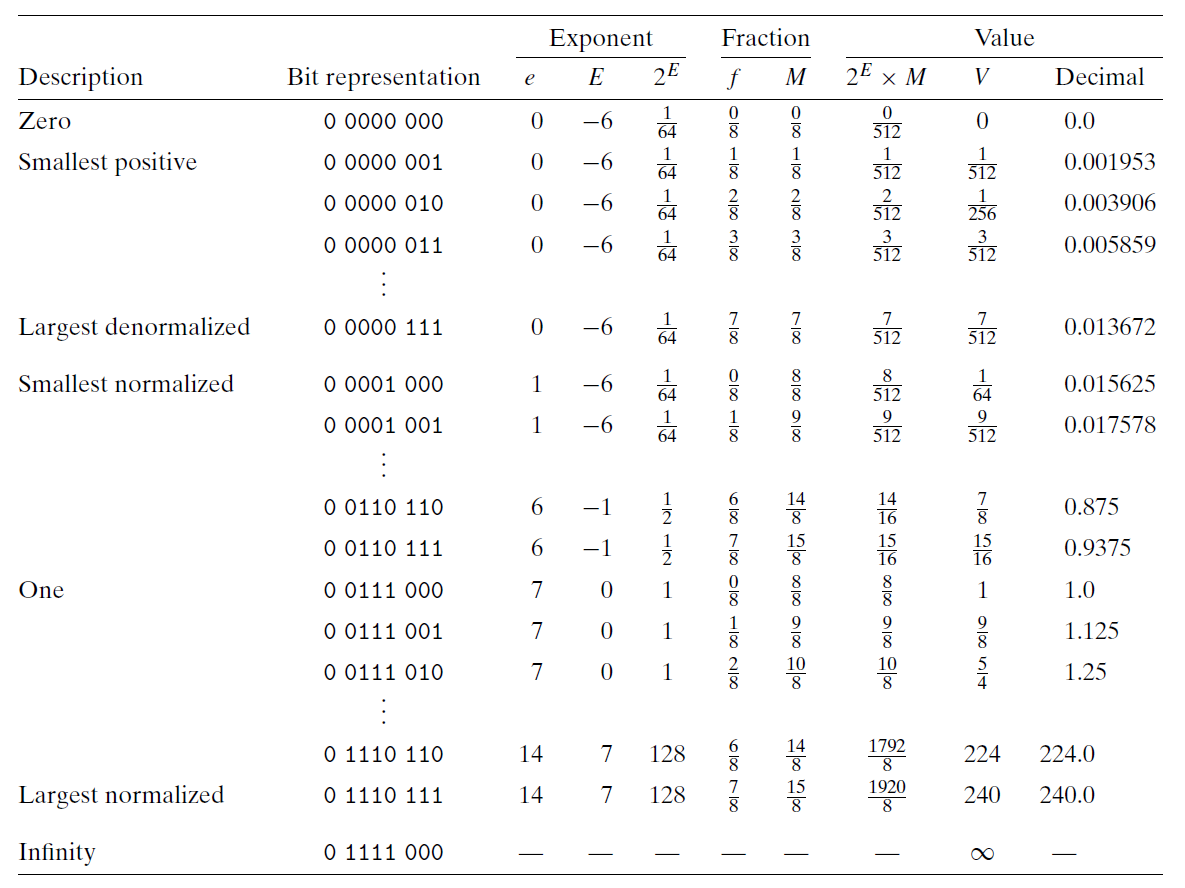
上图被分成了三个区域，来描述三类数字。不同的列给出了阶码字段是如何编码阶码 \(E\) 的，小数字段是如何编码尾数 \(M\) 的，以及它们一起是如何形成要表示的值 \(V = 2^E \times M\) 的。

从 0 自身开始，最靠近 0 的是非规格数（包括 0）.这种格式的非规格化数的 \(E = 1 - 7 = -6\)，得到权 \(2^E = \frac{1}{64}\)。小数 \(f\) 的范围是 \(0, \frac{1}{8}, \cdots, \frac{7}{8}\)，从而得到数 \(V\) 的范围是 \(0 \sim \frac{1}{64} \times \frac{7}{8} = \frac{7}{512}\)。

然后是规格化数。

• 首先是最小规格化数，其 \(E = 1 - 7 = -6\)，和非规格化数是一样的，并且小数的取值范围也是 \(0, \frac{1}{8}, \cdots, \frac{7}{8}\)。然而，其尾数却是在范围 \(1 + 0 = 1\) 和 \(1 + \frac{7}{8} = \frac{15}{8}\) 之间，得出数 \(V\) 在范围 \(\frac{8}{512} = \frac{1}{64}\) 和 \(\frac{15}{512}\) 之间。
  按：这里可以观察到最大非规格化数 \(\frac{7}{512}\) 到最小规格化数 \(\frac{8}{512}\) 之间的平滑转变。这种平滑性归功于我们对非规格化数的 \(E\) 的定义。通过将 \(E\) 定义为 \(1 - Bias\)，而不是 \(-Bias\)，我们通过补偿非规格化数的尾数没有隐含的 1 这样一种方式，达到了既可以表示数值 0 又可以实现平滑转变的目的（平滑转变对浮点数之间的比较大小很有帮助）。
• 当增大阶码时，我们成功地得到更大的规格化数。然后，我们可以得到最大的规格化数，这个数具有阶码 \(E = 7\)，权 \(2^E = 128\)，小数等于 \(\frac{7}{8}\) 得到尾数 \(M = \frac{15}{8}\)，因此，其数值是 \(V = 240\)。超出这个值就会溢出到 \(+\infty\)。

IEEE 的这种表示具有一个有趣的属性，我们可以发现上面 8 位浮点格式的非负值示例表格中的数据，如果把它们的位表达式看成是无符号整数，那么它们从上到下是按照升序的方式排列的，而它们所表示的浮点数也是升序排列的。IEEE 这样设计的目的其实就是为了让浮点数能够使用整数排序来进行排序。当比较负数时，同样可以使用类似的方法。

还有一点要注意的地方，就是 IEEE754 这个阶码的部分（e），它是用移码来表示的，关于移码，可以参看另一篇博客。

4. 例题

例1 将十进制数 20.59375 转换成 32 位 IEEE754 格式浮点数的二进制格式来存储。

解：先将十进制数转换成二进制数：

\[ 20.59375 = 10100.10011 \; (0.5 + 0.25 + 0.125 + 0.0625 + 0.03125) \]

移动小数点，使其变成 \(1.M\) 的形式：

\[ 10100.10011 = 1.010010011 \times 2^4 \]

得到：

\[ S = 0, e = 4, E = 100_2 + 01111111_2 = 10000011_2, M = 010010011 \]

最后得到 32 位浮点数的二进制存储格式为：

\[ \begin{split} &0100 \; 0001 \; 1010 \; 0100 \; 1100 \; 0000 \; 0000 \; 0000 \\ &= (41A4C000)_16 \end{split} \]

例2 若某浮点数 x 的二进制存储格式为 \((41360000)_16\)，求与其对应的 32 位浮点表示的十进的值。

解：

首先判断是规格数。

然后进行处理，

\[ \begin{split} &(41360000)_16 \\ &= (0 \; 100,0001,0 \; 011,0110,0000,0000,0000,0000)_2 \end{split} \]

由此可得：

\[ \begin{split} &s = 0 \\ &E = e - Bias = 10000010 - 01111111 = &00000011 = (3)_10 \\ &M = 1.011011 \end{split} \]

则上述浮点数对应的真值为

\[ V = (-1)^s \times M \times 2^E = (-1)^0 \times 2^3 = 1011.011 = (11.375)_10 \]

---

参考：

1、《深入理解计算机系统 第三版》