编译原理作业二
系第三章课后作业(仅限布置作业的部分)。
1、构造下列正规式相应的 \(\text{DFA}\)。
(1) \(1(0|1)^*101\)
解:先构造 \(\text{NFA}\)

然后,用子集法将 \(\text{NFA}\) 确定化

除 X, A 外,重新命名其他状态,令 AB 为 B、AC 为 C、ABY 为 D,因为 D 含有 Y(NFA 的终态),所以 D 为终态。

DFA 的状态图:

3、将下图的 NFA 确定化。
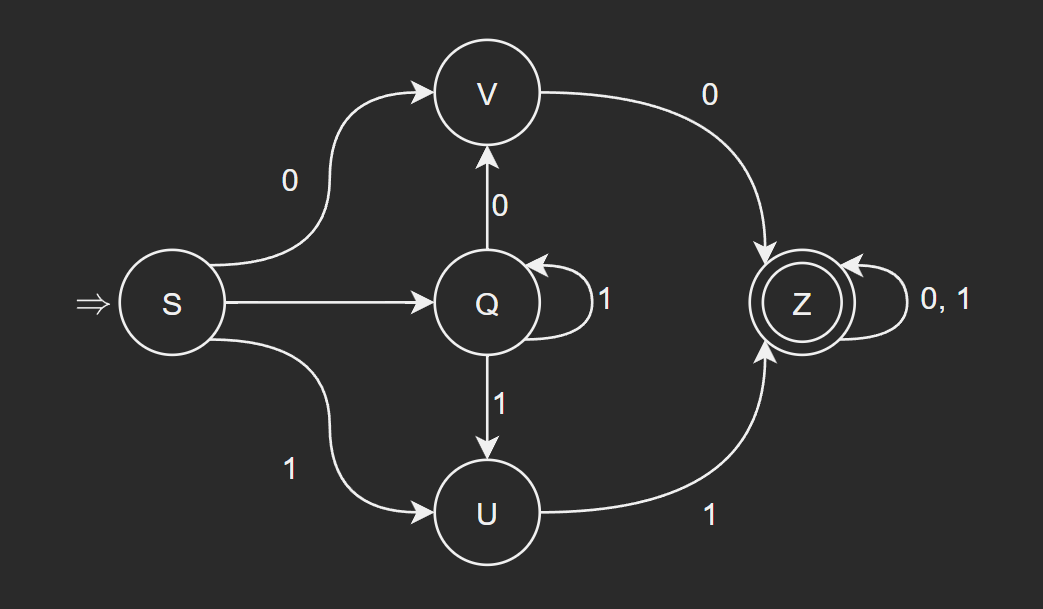
解:用子集法将 NFA 确定化:

重新命名状态子集,令 VQ 为 A、QU 为 B、VZ 为 C、V 为 D、QUZ 为 E、Z 为 F。
DFA 的状态图:

7、为正规文法 \(G[S]\)
\[ \begin{split} S &\rightarrow aA|bQ \\ A &\rightarrow aA|bB|b \\ B &\rightarrow bD|aQ \\ Q &\rightarrow aQ|bD|b \\ D &\rightarrow bB|aA \\ E &\rightarrow aB|bF \\ F &\rightarrow bD|aE|b \end{split} \]
构造相应的最小的 \(\text{DFA}\)。
解:先构造其 NFA:

用子集法将 NFA 确定化:

将 S、A、Q、BZ、DZ、D、B 重新命名,分别用 0、1、2、3、4、5、6 表示。因为 3、4 中含有 z,所以它们为终态。

DFA 的状态图如下:

令 \(P_0 = (\{0, 1, 2, 5, 6\}, \{3,
4\})\) 用 b 进行分割;
\(P_1 = (\{0, 5, 6\}, \{1, 2\}, \{3,
4\})\) 再用 b 进行分割;
\(P_2 = (\{0\}, \{5, 6\}, \{1, 2\}, \{3,
4\})\) 再用 a、b 进行分割,仍不变。
再令 \(\{0\}\) 为 A,\(\{1, 2\}\) 为 B,\(\{3, 4\}\) 为 C,\(\{5, 6\}\) 为 D。
最小化为:

11、有一种用以证明两个正规表达式等价的方法,那就是构造它们的最小 DFA,表明这两个 DFA 是一样的(除了状态名不同外)。使用此方法。证明下面的正规表达式是等价的。
\[ \begin{split} (1)& \; (a|b)^* \\ (2)& \; (a^* | b^*)^* \\ \end{split} \]
解:
(1) 的 NFA 图如下

根据 NFA 构造最小的 DFA 如下:

(2) 的 NFA 图如下

根据 NFA 构造最小的 DFA 如下:

所以,由此可以证明 (1) 和 (2) 式正规式是等价的。