编译原理作业三

系第四章课后作业（部分）。

1、对文法 \(G[S]\)

\[ \begin{split} S &\rightarrow a | \wedge | (T) \\ T &\rightarrow T, S | S \end{split} \]

(1) 给出 \((a, (a, a))\) 和 \((((a, a), \wedge, (a)), a)\) 的最左推导。
(2) 对文法 \(G\) 进行改写，然后对每个非终结符写出不带回溯的递归子程序。
(3) 经改写后的文法是否是 \(LL(1)\) 的？给出它的预测分析表。
(4) 给出输入串 \((a, a)＃\) 的分析过程，并说明该串是否为 \(G\) 的句子。

解：

(1) 对 \((a, (a, a))\) 的最左推导为：

\[ \begin{split} S &\Rightarrow (T) \\ &\Rightarrow (T, S) \\ &\Rightarrow (S, S) \\ &\Rightarrow (a, S) \\ &\Rightarrow (a, (T)) \\ &\Rightarrow (a, (T, S)) \\ &\Rightarrow (a, (S, S)) \\ &\Rightarrow (a, (a, S)) \\ &\Rightarrow (a, (a, a)) &\end{split} \]

对 \((((a, a), \wedge, (a)), a)\) 的最左推导如下：

\[ \begin{split} S &\Rightarrow (T) \\ &\Rightarrow (T, S) \\ &\Rightarrow (S, S) \\ &\Rightarrow ((T), S) \\ &\Rightarrow ((T, S), S) \\ &\Rightarrow ((T, S, S), S) \\ &\Rightarrow (((S, S), S, S), S) \\ &\Rightarrow (((a, S), S, S), S) \\ &\Rightarrow (((a, a), S, S), S) \\ &\Rightarrow (((a, a), \wedge, S), S) \\ &\Rightarrow (((a, a), \wedge, (T)), S) \\ &\Rightarrow (((a, a), \wedge, (S)), S) \\ &\Rightarrow (((a, a), \wedge, (a)), S) \\ &\Rightarrow (((a, a), \wedge, (a)), a) \\ \end{split} \]

(2) 改写文法为：

\[ \begin{split} (0) &S \rightarrow a \\ (1) &S \rightarrow \wedge \\ (2) &S \rightarrow (T) \\ (3) &T \rightarrow SN \\ (4) &N \rightarrow ,S N \\ (5) &N \rightarrow \varepsilon \end{split} \]

对每个非终结符，其不带回溯的递归子程序如下：

PROCEDURE S(TOKEN);
BEGIN
    IF TOKEN != 'a' AND TOKEN != '∧' THEN
        BEGIN
            IF TOKEN = '(' THEN
                BEGIN
                    GETNEXT(TOKEN);
                    T(TOKEN);
                    GETNEXT(TOKEN);
                    IF TOKEN != ')' THEN ERROR
                END
            ELSE ERROR
        END
END

PROCEDURE T(TOKEN);
BEGIN
    S(TOKEN);
    N(TOKEN);
END

PROCEDURE N(TOKEN);
BEGIN
    IF TOKEN = ',' THEN
        BEGIN
            GETNEXT(TOKEN);
            S(TOKEN);
            N(TOKEN);
        END
END

(3) 经改写后的文法是 \(LL(1)\) 文法，

对改写后的文法，求其 \(FIRST\) 集、\(FOLLOW\) 集、\(SELECT\) 集如下：

符号	\(FIRST\)	\(FOLLOW\)
\(S\)	\(\{A, \wedge, (\}\)	\(\#, , , )\)
\(T\)	\(\{a, \wedge, (\}\)	\(\{ ) \}\)
\(N\)	\(\{, , \varepsilon\}\)	\(\{ ) \}\)

\[ \begin{split} &SELECT(0) = \{ a \} \\ &SELECT(1) = \{ \wedge \} \\ &SELECT(2) = \{ ( \} \\ &SELECT(3) = \{ a, \wedge, ( \} \\ &SELECT(4) = \{ , \} \\ &SELECT(5) = \{ ) \} \\ \end{split} \]

它的预测分析表如下：

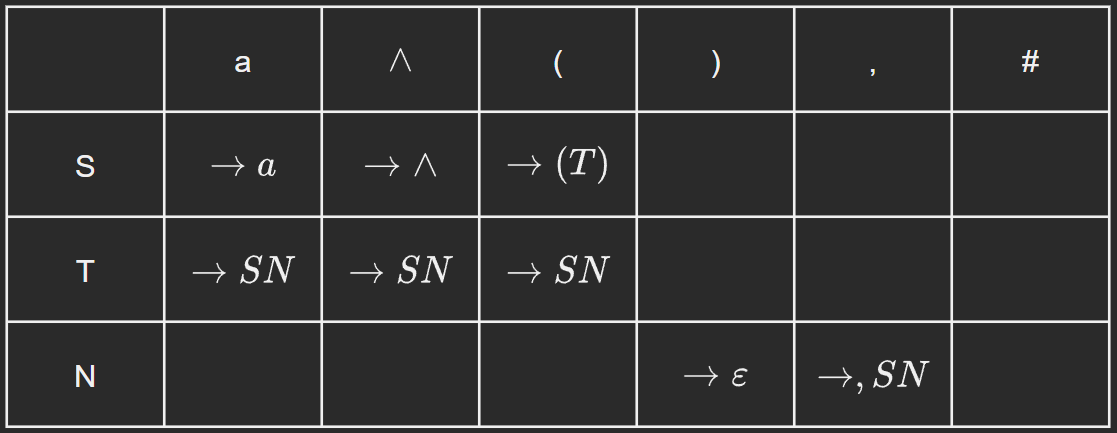
(4) 对输入串 \((a, a)＃\) 的分析过程如下：

栈	当前输入符	剩余输入符	所用产生式
#S	(	a,a)#	S \(\rightarrow\) (T)
#)T(	(	a,a)#
#)T	a	,a)#	T \(\rightarrow\) SN, S \(\rightarrow\) a
#)NS	a	,a)#
#)Na	a	,a)#
#)N	,	a)#	N \(\rightarrow\),SN
#)NS,	,	a)#
#)NS	a	)#	S \(\rightarrow\) a
#)Na	a	)#
#)N	)	#	N \(\rightarrow \varepsilon\)
#)	)	#
#	#

可见输入串 \((a, a)＃\) 是文法的句子。

4、证明下述文法不是 \(LL(1)\) 的。

\[ \begin{split} S &\rightarrow C\$ \\ C &\rightarrow bA | aB \\ A &\rightarrow a | aC | bAA \\ B &\rightarrow b | bC | aBB \end{split} \]

能否构造一等价的文法，使其是 \(LL(1)\) 的？并给出判断过程。

解：

题中文法的 SELECT 集如下：

\[ \begin{split} &SELECT(S \rightarrow C\$) = \{b, a\} \\ &SELECT(A \rightarrow a) = \{a\} \\ &SELECT(A \rightarrow aC) = \{a\} \\ &SELECT(A \rightarrow bAA) = \{b\} \\ &SELECT(C \rightarrow bA) = \{b\} \\ &SELECT(C \rightarrow aB) = \{a\} \\ &SELECT(B \rightarrow b) = \{b\} \\ &SELECT(B \rightarrow bc) = \{b\} \\ &SELECT(B \rightarrow aBB) = \{a\} \\ \end{split} \]

由于

\[ SELECT(A \rightarrow a) \cap SELECT(A \rightarrow ac) \cap SELECT(A \rightarrow bAA) \neq \varnothing \]

所以该文法不是 \(LL(1)\) 文法。

构造等价文法如下：

\[ \begin{split} S &\rightarrow C\$ \\ C &\rightarrow bA | aB \\ A &\rightarrow aN | bAA \\ B &\rightarrow bN | aBB \\ N &\rightarrow C | \varepsilon \end{split} \]

计算 \(SELECT\) 集如下：

\[ \begin{split} &SELECT(S \rightarrow C\$) = \{b, a\} \\ &SELECT(C \rightarrow bA) = \{b\} \\ &SELECT(C \rightarrow aB) = \{a\} \\ &SELECT(A \rightarrow aN) = \{a\} \\ &SELECT(A \rightarrow bAA) = \{b\} \\ &SELECT(B \rightarrow bN) = \{b\} \\ &SELECT(B \rightarrow aBB) = \{a\} \\ &SELECT(N \rightarrow C) = \{b, a\} \\ &SELECT(N \rightarrow \varepsilon) = \{a, b\} \\ \end{split} \]

由于

\[ SELECT(N \rightarrow C) \cap SELECT(N \rightarrow \varepsilon) \neq \varnothing \]

所以改写后的文法不是 \(LL(1)\) 文法。

7、对于一个文法若消除了左递归，提取了左公共因子后是否一定为 \(LL(1)\) 文法？试对下面的文法进行改写，并对改写后的文法进行判断。

\[ \begin{split} (4) S &\rightarrow AS | b \\ A &\rightarrow SA | a \end{split} \]

解：对文法进行改写如下：

\[ \begin{split} S &\rightarrow AS | b \\ A &\rightarrow baA^{'} | aA^{'} \\ A^{'} &\rightarrow SAA^{'} | \varepsilon \end{split} \]

首先，消除左递归，

\[ \begin{split} &(0) \; S \rightarrow AS \\ &(1) \;S \rightarrow b \\ &(2) \;A \rightarrow baA^{'}\\ &(3) \;A \rightarrow aA^{'} \\ &(4) \;A^{'} \rightarrow SAA^{'} \\ &(5) \;A^{'} \rightarrow \varepsilon \end{split} \]

然后，提取隐式公共因子，

然后计算各个符号的 \(FIRST\) 集、\(FOLLOW\) 集 以及文法的 \(SELECT\) 集：

符号	\(FIRST\)	\(FOLLOW\)
\(S\)	\(\{a, b\}\)	\(\{a, b\}\)
\(A\)	\(\{a, b\}\)	\(\{a, b\}\)
\(A^{'}\)	\(\{a, b, \varepsilon\}\)	\(\{a, b\}\)

\[ \begin{split} &SELECT(0) = \{ a, b \} \\ &SELECT(1) = \{ b \} \\ &SELECT(2) = \{ b \} \\ &SELECT(3) = \{ a \} \\ &SELECT(4) = \{ a, b \} \\ &SELECT(5) = \{ a, b \} \\ \end{split} \]

由于

\[ SELECT(0) \cap SELECT(1) \neq \varnothing \]

所以改写后的文法不是 \(LL(1)\) 文法。