利用 Python 替换字符

之前读《算法竞赛入门经典（第 2 版）》的时候，以为算法没什么用，现在发现其实还挺有用的，简单的题目就很有用，比如替换字符啦，比如整一些加密啦。

现在就有一个需求，之前用的 Hexo 框架的数学插件写行内数学公式需要在 $ 左右再加上一对反引号，现在我用的是另一个数学插件，它不需要加反引号，所以有些之前的文章就需要把反引号给去掉。这里，Python 就派上了用场。

raw_str = """
## 1、图的定义

图（Graph）是由两个集合构成，一个是非空但有限的顶点集合 $V$，另一个是描述顶点之间关系——边的集合 $E$（可以是 $\varnothing$）。因此，图可以表示为 $G = (V, E)$。每条边是一顶点对 $(v, w)$ 且 $v, w \in V$。

通常用 $|V|$ 表示顶点的数量，用 $|E|$ 表示边的数量。

## 2、图的术语

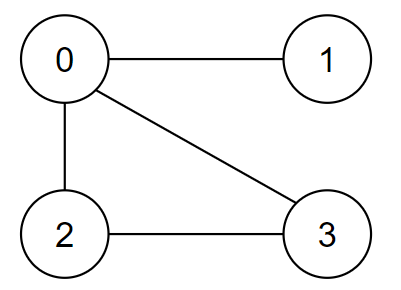
(1)、无向图（Underected Graphs）：无向图中顶点之间的边（Edge）没有方向，即边 $(v, w)$ 等同于 $(w, v)$。用圆括号“()”表示无向边。边的起点 $w$ 和终点 $v$ 次序并不重要。

![图一　　无向图](https://cdn.jsdelivr.net/gh/fanlumaster/BlogMaps@master/blogs/pictures/20210608212819.png)

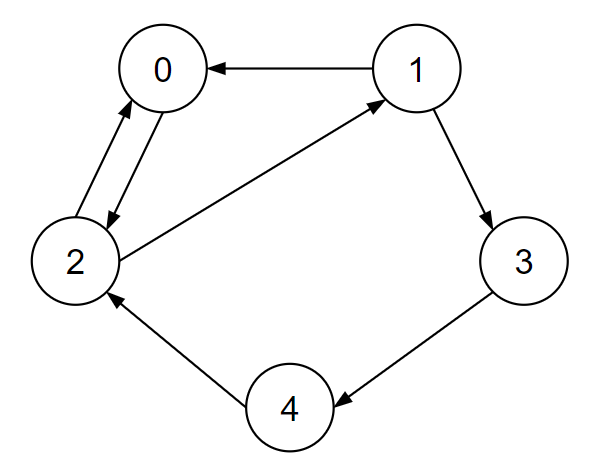
(2)、有向图（Directed Graphs）：有向图中顶点之间的所有边都有方向，即 $<v, w>$ 不同于 $<w, v>$。用尖括号“<>”表示有向边。有向边也称弧（Are）。弧的“起点（弧头）”和“终点（弧尾）”的次序不能随意颠倒。在不会混淆的场合，有向边和无向边都简称为“边”。

![图二　　有向图](https://cdn.jsdelivr.net/gh/fanlumaster/BlogMaps@master/blogs/pictures/20210608213830.png)

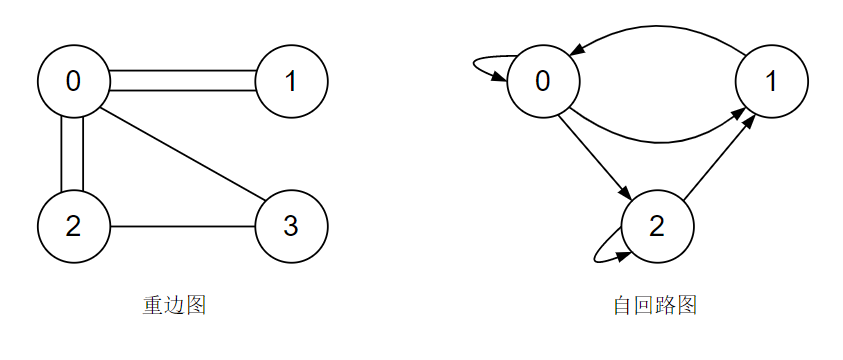
(3)、简单图（Simple Graph）：如果图中出现重边（即边的集合 $E$ 中有相同的重复元素）或者自回路边（即边的起点和终点是同一个顶点），就叫做非简单图。

![图三　　两种非简单图](https://cdn.jsdelivr.net/gh/fanlumaster/BlogMaps@master/blogs/pictures/20210608220507.png)

(4)、邻接点（Adjacent Vertices）：如果 $(v, w)$ 是无向图中任意一条边，那么称 $v$ 和 $w$ 互为邻接点；如果 $<v, w>$ 是有向图中任意一条边，那么称起点 `$v$` “邻接到”（Adjacent to）终点 `$w$`，也称终点 `$w$` “邻接自”（Adjacent from）起点 `$v$`。比如，考察图二这个有向图 `$G_2$`，顶点 2 邻接到顶点 1，或者说顶点 1 邻接自顶点 2。

(5)、路径（Path）、简单路径（Simple Path）、回路（Cycle，也叫做“环”）、无环图（Acyclic Graph）：图中的一条路径是一顶点序列 `$v_1, v_2, ..., v_N$`，序列中任何相邻的两顶点都能在图中找到对应的边，即 `$(v_i, v_{i + 1}) \in E (1 \leqslant i < N)$`。一条路径的长度是这条路径所包含的边数。

一条**简单路径**是指除了路径的首尾顶点外，其余顶点都是不同的。

有向图中的一条回路是指 `$v_1 = v_N$` 的一条路径。路径长度为 1 的回路是一个自回路（属于非简单图）。简单路径形成的回路称为简单回路（Simple Cycle）。

如果在一个有向图中不存在回路，那么这个有向图称为无环图。

对于无向图，由于顶点是无序的，环路的长度要大于等于 3。

按：本文所有术语和定义皆摘自浙江大学《数据结构 第二版》（陈越、何钦铭），且省略了部分我认为不重要的内容。

(12)、连通图（Connected Graph）、连通分量（Connected Component）：在无向图中，如果从一个顶点 `$v_i$` 到另一个顶点 `$v_j(i \leq j)$` 有路径，则称顶点 `$v_i$` 和 `$v_j$` 是连通的（Connected）。如果图中任意两顶点都是连通的，则称该图是连通图。无向图的极大连通子图称为连通分量。连通分量的概念包含以下 4 个要点：

- 子图：连通分量应该是原图的子图；
- 连通：连通分量本身应该是连通的；
- 极大顶点数：连通子图含有极大顶点数，即再加入其他顶点将会导致子图不连通；
- 极大边数：具有极大顶点数的连通子图包含依附于这些顶点的所有边。

因此，连通的无向图只有一个连通分量，这个连通分量就是本图。不连通的无向图有多于一个的连通分量。

(13)、强连通图（Strongly Connected Graph）、强连通分量（Strongly Connected Component）；对于有向图来说，若图中任意一对顶点 `$v_i$` 和 `$v_j(i \leq j)$` 均既有从 `$v_i$` 到 `$v_j$` 的路径，也有从 `$v_j$` 到 `$v_i$` 的路径，则称该有向图是强连通图。有向图的极大强连通子图称为强连通分量。

强连通分量的概念与连通分量类似，也包含 4 个要点。强连通图本身就是一个强连通分量。不是强连通的有向图有多于一个的强连通分量。
"""

reverted_str = """"""
count = 0

for i in raw_str:
    if i == '`':
        # print(i)
        count = count + 1
        continue
    reverted_str = reverted_str + i

print(reverted_str)

print(len(raw_str))
print(len(reverted_str))
print(count)

按：这里只作了简答的替换，以后有需要的时候会更新。